Hi All, I am learning Finite Difference Method and try to solve following equation.
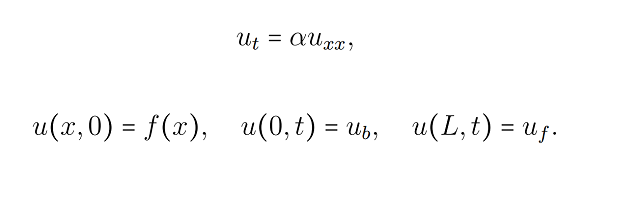
for f(x)=sin(pi x), ub=0=uf, L=1, alpha=1/20
we know exact solution is
u[x_, t_] := Sin[(\[Pi] x)/L] E^(-((\[Alpha] \[Pi]^2 t)/L^2))
Here what I did so far
L = 1;
n = 50;(*num interior points*)
\[CapitalDelta]x = L/n;
\[CapitalDelta]t = 0.002;(*cfl:dt/dx^2\[LessEqual].5*)
\[Alpha] = 1./20;
\[Alpha] \[CapitalDelta]t/\[CapitalDelta]x^2
0.25
T[i_, 0] := Sin[\[Pi] i \[CapitalDelta]x](*initial value*)
T[0, j_] := 0;(*boundaries*)
T[1, j_] := 0.;(*boundaries*)
T[i_, j_] :=T[i, j] = T[i, j - 1] + \[Alpha] \[CapitalDelta]t/\[CapitalDelta]x^2 (T[i + 1, j - 1] - 2 T[i, j - 1] + T[i - 1, j - 1]);
s = Table[T[i, j], {j, 1, n}, {i, 1, n}];
ListPointPlot3D[s]
My second approach is
n = 6; \[Alpha] = 1/20; L = 1; BC1 = 0; BC2 = 0;
\[CapitalDelta]x = L/(n - 1.)
\[CapitalDelta]t = 4/(n - 1.)
r = \[Alpha] \[CapitalDelta]t/\[CapitalDelta]x ^2
U[t_] = Table[Subscript[U, i], {i, 0, n}]
IC = Thread[U[0] == (Sin[\[Pi] #] & /@ Range[0., 1, (1 - 0)/n])]
A = SparseArray[{{n , n } -> 1., {i_, i_} -> (1 - 2. r), {i_, j_} /; Abs[i - j] == 1 -> r}, {n - 1, n - 1}, 0.];
But I am lost, don't know how to apply IC and BC for the matrix set up to solve the system..
Any suggestion? Thanks in advance..