Hi Jonathan,
I guess that to really help you, I would need your data file - or something quite similar to it. I can only show you how this works in principle. So these are the data points you give:
data = {{2, 2, 8}, {4, 4, 16}, {5, 5, 10}, {-1, 8, 40}, {0.7, 4, -100}};
The next thing we need is a reasonable model. This step is a bit of "art". You can plot the data with
ListPointPlot3D[data, PlotStyle -> Directive[Red, PointSize[0.02]]]
to get an idea of what you might want. I thought that it might come from something like this:
model = a x + b y + c Abs[x] + d Abs[y] + e Abs[x + y]
You can then find parameters
params = FindFit[data, model, {a, b, c, d, e}, {x, y}]
and plot everything
Show[Plot3D[model /. params, {x, -2, 6}, {y, 2, 9}], ListPointPlot3D[data, PlotStyle -> Directive[Red, PointSize[0.02]]]]
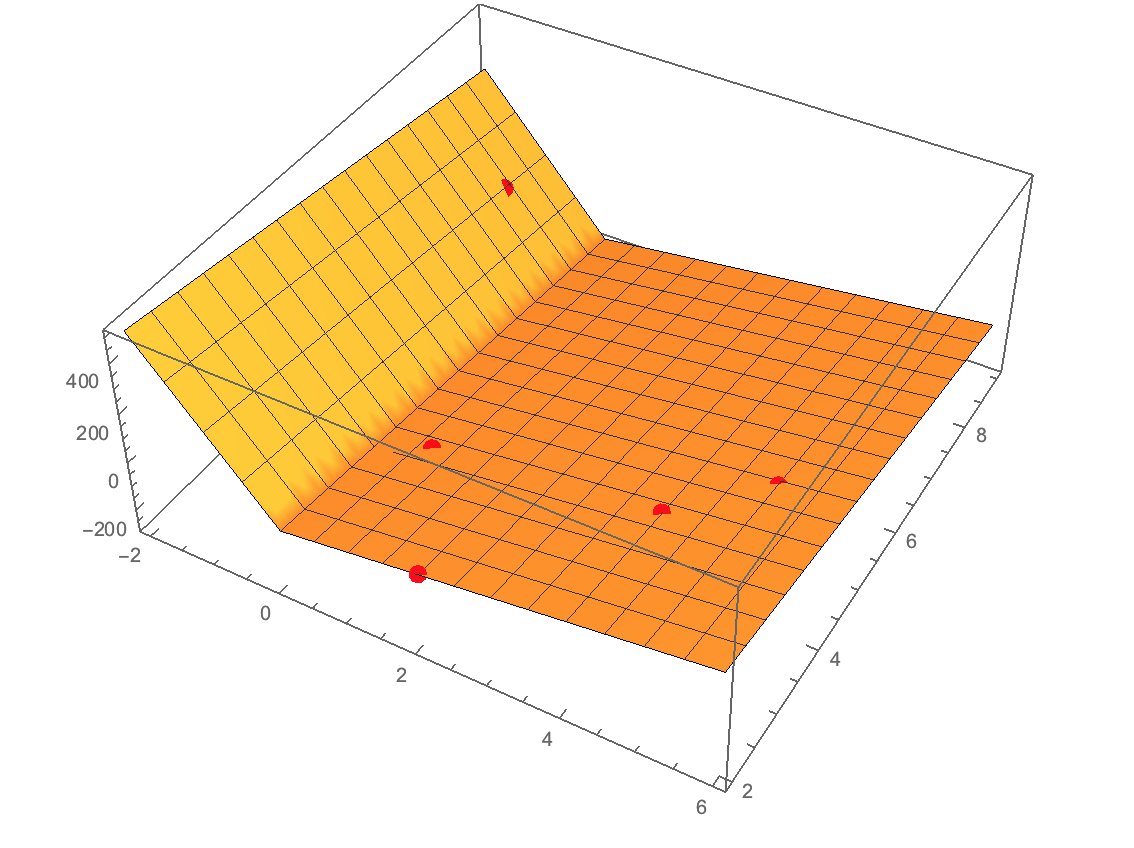
It also becomes quite clear that this is not really easy to fit: 4 points are nearly in a plane. There is only one which is out of the plane and there are many ways of getting a good fit. I also use too many parameters for this fit. There are 5 points and 5 parameters, which is obviously not really ideal.
Cheers,
Marco