A cuboid makes use of three rectangles, each used twice. Is it possible to make a polyhedron where all the rectangles are distinct?
I found a 30 rectangle solution.
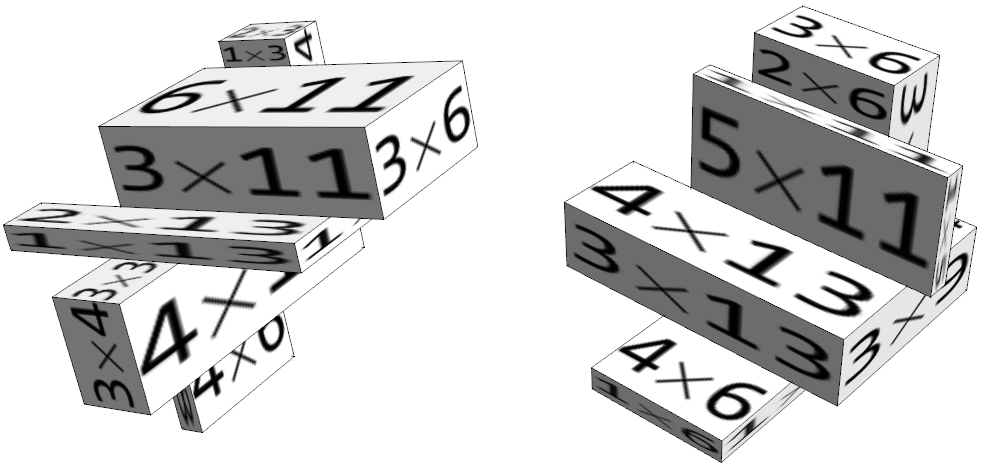
Here's some raw data for that image:
dat={
{"1\[Times]1",{{8,14,9},{8,14,8},{8,13,8},{8,13,9}},{{0,0},{1,0},{1,1},{0,1}}},
{"1\[Times]11",{{13,3,9},{13,3,8},{13,14,8},{13,14,9}},{{0,1},{0,0},{1,0},{1,1}}},
{"1\[Times]12",{{4,11,12},{4,11,0},{5,11,0},{5,11,12}},{{1,0},{0,0},{0,1},{1,1}}},
{"1\[Times]13",{{13,3,9},{13,3,8},{0,3,8},{0,3,9}},{{1,1},{1,0},{0,0},{0,1}}},
{"1\[Times]2",{{0,3,9},{0,3,8},{0,5,8},{0,5,9}},{{0,0},{0,1},{1,1},{1,0}}},
{"1\[Times]3",{{8,11,13},{5,11,13},{5,11,12},{8,11,12}},{{1,1},{0,1},{0,0},{1,0}}},
{"1\[Times]4",{{4,5,9},{4,5,8},{0,5,8},{0,5,9}},{{0,1},{0,0},{1,0},{1,1}}},
{"1\[Times]5",{{13,14,9},{13,14,8},{8,14,8},{8,14,9}},{{0,1},{0,0},{1,0},{1,1}}},
{"1\[Times]6",{{4,11,0},{4,5,0},{5,5,0},{5,11,0}},{{1,0},{0,0},{0,1},{1,1}}},
{"1\[Times]8",{{4,5,8},{4,5,0},{5,5,0},{5,5,8}},{{0,0},{1,0},{1,1},{0,1}}},
{"2\[Times]13",{{13,3,9},{0,3,9},{0,5,9},{13,5,9}},{{1,0},{0,0},{0,1},{1,1}}},
{"2\[Times]3",{{8,13,13},{5,13,13},{5,11,13},{8,11,13}},{{1,1},{0,1},{0,0},{1,0}}},
{"2\[Times]4",{{8,13,9},{8,11,9},{8,11,13},{8,13,13}},{{0,0},{0,1},{1,1},{1,0}}},
{"2\[Times]5",{{5,3,8},{0,3,8},{0,5,8},{5,5,8}},{{0,0},{1,0},{1,1},{0,1}}},
{"2\[Times]6",{{15,11,9},{15,5,9},{13,5,9},{13,11,9}},{{1,1},{0,1},{0,0},{1,0}}},
{"2\[Times]9",{{5,13,4},{5,11,4},{5,11,13},{5,13,13}},{{0,1},{0,0},{1,0},{1,1}}},
{"3\[Times]11",{{4,5,12},{4,5,9},{15,5,9},{15,5,12}},{{0,1},{0,0},{1,0},{1,1}}},
{"3\[Times]13",{{8,13,4},{5,13,4},{5,0,4},{8,0,4}},{{1,1},{1,0},{0,0},{0,1}}},
{"3\[Times]3",{{8,3,8},{5,3,8},{5,0,8},{8,0,8}},{{1,0},{1,1},{0,1},{0,0}}},
{"3\[Times]4",{{8,0,4},{5,0,4},{5,0,8},{8,0,8}},{{0,0},{0,1},{1,1},{1,0}}},
{"3\[Times]5",{{13,11,9},{8,11,9},{8,14,9},{13,14,9}},{{1,0},{0,0},{0,1},{1,1}}},
{"3\[Times]6",{{15,11,12},{15,5,12},{15,5,9},{15,11,9}},{{1,1},{0,1},{0,0},{1,0}}},
{"3\[Times]7",{{8,11,12},{8,11,9},{15,11,9},{15,11,12}},{{1,1},{1,0},{0,0},{0,1}}},
{"3\[Times]9",{{8,13,4},{5,13,4},{5,13,13},{8,13,13}},{{0,1},{0,0},{1,0},{1,1}}},
{"4\[Times]13",{{8,13,4},{8,0,4},{8,0,8},{8,13,8}},{{1,0},{0,0},{0,1},{1,1}}},
{"4\[Times]5",{{5,5,4},{5,0,4},{5,0,8},{5,5,8}},{{1,1},{0,1},{0,0},{1,0}}},
{"4\[Times]6",{{5,11,4},{5,5,4},{5,5,0},{5,11,0}},{{1,1},{0,1},{0,0},{1,0}}},
{"5\[Times]11",{{13,3,8},{8,3,8},{8,14,8},{13,14,8}},{{0,1},{0,0},{1,0},{1,1}}},
{"6\[Times]11",{{4,11,12},{4,5,12},{15,5,12},{15,11,12}},{{0,1},{0,0},{1,0},{1,1}}},
{"6\[Times]12",{{4,11,12},{4,5,12},{4,5,0},{4,11,0}},{{1,1},{1,0},{0,0},{0,1}}}};
Textures can be used to put the size of each rectangle on the appropriate face.
obj = Graphics3D[
Table[{Texture[
Image[Rasterize[Style[dat[[n, 1]], 40], RasterSize -> 1200]]],
Polygon[dat[[n, 2]],
VertexTextureCoordinates -> dat[[n, 3]]]}, {n, 1, 30}],
Lighting -> "Neutral", Boxed -> False, SphericalRegion -> True,
ImageSize -> {500, 500}, ViewAngle -> Pi/9];
Then I just need to make a row of the graphics, and turn them to make an appropriate image.
Row[{obj, obj}]
My method for finding this was to look at polycubes. A cuboid has three repeats, so a solution made of cuboids would require that each touch three others. The L-polycube doesn't necessarily repeat any rectangles, but has two non-rectangular faces that need to be broken. There might be a L-cuboid solution where each touches 2 others. It exists, but needs 30 rectangles. I made the below function for it. I then had Mathematica do a large random search, and the input {4, 1, 3, 5, 2, 3, 2, 6, 2, 1, 4, 4, 1, 3, 1} seemed like the optimal solution.
thirtyrects[{a1_,a2_,a3_,a4_,a5_,b1_,b2_,b3_,b4_,b5_,c1_,c2_,c3_,c4_,c5_}]:=
{{{0,b1,c1+c2+c3},{0,b1,c1+c2},{0,b1+b2,c1+c2},{0,b1+b2,c1+c2+c3}},
{{a1,b1+b2+b3,c1+c2+c3+c4},{a1,b1+b2,c1+c2+c3+c4},{a1,b1+b2,0},{a1,b1+b2+b3,0}},
{{a1+a2,b1+b2,c1},{a1+a2,0,c1},{a1+a2,0,c1+c2},{a1+a2,b1+b2,c1+c2}},
{{a1+a2,b1+b2+b3,c1},{a1+a2,b1+b2,c1},{a1+a2,b1+b2,0},{a1+a2,b1+b2+b3,0}},
{{a1+a2,b1+b2+b3+b4,c1},{a1+a2,b1+b2+b3,c1},{a1+a2,b1+b2+b3,c1+c2+c3+c4+c5},{a1+a2,b1+b2+b3+b4,c1+c2+c3+c4+c5}},
{{a1+a2+a3,b1+b2+b3+b4,c1},{a1+a2+a3,0,c1},{a1+a2+a3,0,c1+c2},{a1+a2+a3,b1+b2+b3+b4,c1+c2}},
{{a1+a2+a3,b1+b2+b3+b4,c1+c2+c3},{a1+a2+a3,b1+b2+b3,c1+c2+c3},{a1+a2+a3,b1+b2+b3,c1+c2+c3+c4+c5},{a1+a2+a3,b1+b2+b3+b4,c1+c2+c3+c4+c5}},
{{a1+a2+a3,b1+b2+b3+b4+b5,c1+c2+c3},{a1+a2+a3,b1+b2+b3+b4+b5,c1+c2},{a1+a2+a3,b1+b2+b3+b4,c1+c2},{a1+a2+a3,b1+b2+b3+b4,c1+c2+c3}},
{{a1+a2+a3+a4,b1,c1+c2+c3},{a1+a2+a3+a4,b1,c1+c2},{a1+a2+a3+a4,b1+b2+b3+b4+b5,c1+c2},{a1+a2+a3+a4,b1+b2+b3+b4+b5,c1+c2+c3}},
{{a1+a2+a3+a4+a5,b1+b2+b3,c1+c2+c3+c4},{a1+a2+a3+a4+a5,b1+b2,c1+c2+c3+c4},{a1+a2+a3+a4+a5,b1+b2,c1+c2+c3},{a1+a2+a3+a4+a5,b1+b2+b3,c1+c2+c3}},
{{a1,b1+b2,c1+c2},{a1,b1+b2,0},{a1+a2,b1+b2,0},{a1+a2,b1+b2,c1+c2}},
{{a1,b1+b2,c1+c2+c3+c4},{a1,b1+b2,c1+c2+c3},{a1+a2+a3+a4+a5,b1+b2,c1+c2+c3},{a1+a2+a3+a4+a5,b1+b2,c1+c2+c3+c4}},
{{a1,b1+b2+b3,c1+c2+c3+c4},{a1,b1+b2+b3,0},{a1+a2,b1+b2+b3,0},{a1+a2,b1+b2+b3,c1+c2+c3+c4}},{{a1+a2+a3,0,c1},{a1+a2,0,c1},{a1+a2,0,c1+c2},{a1+a2+a3,0,c1+c2}},
{{a1,b1+b2,c1+c2+c3},{a1,b1+b2,c1+c2},{0,b1+b2,c1+c2},{0,b1+b2,c1+c2+c3}},
{{a1+a2+a3,b1+b2+b3,c1+c2+c3+c4},{a1+a2+a3,b1+b2+b3,c1+c2+c3},{a1+a2+a3+a4+a5,b1+b2+b3,c1+c2+c3},{a1+a2+a3+a4+a5,b1+b2+b3,c1+c2+c3+c4}},
{{a1+a2+a3,b1+b2+b3,c1+c2+c3+c4+c5},{a1+a2,b1+b2+b3,c1+c2+c3+c4+c5},{a1+a2,b1+b2+b3,c1+c2+c3+c4},{a1+a2+a3,b1+b2+b3,c1+c2+c3+c4}},
{{a1+a2+a3,b1+b2+b3+b4,c1},{a1+a2,b1+b2+b3+b4,c1},{a1+a2,b1+b2+b3+b4,c1+c2+c3+c4+c5},{a1+a2+a3,b1+b2+b3+b4,c1+c2+c3+c4+c5}},
{{a1+a2+a3+a4,b1,c1+c2+c3},{a1+a2+a3+a4,b1,c1+c2},{0,b1,c1+c2},{0,b1,c1+c2+c3}},
{{a1+a2+a3+a4,b1+b2+b3+b4+b5,c1+c2+c3},{a1+a2+a3+a4,b1+b2+b3+b4+b5,c1+c2},{a1+a2+a3,b1+b2+b3+b4+b5,c1+c2},{a1+a2+a3,b1+b2+b3+b4+b5,c1+c2+c3}},
{{a1,b1+b2+b3,0},{a1,b1+b2,0},{a1+a2,b1+b2,0},{a1+a2,b1+b2+b3,0}},
{{a1,b1+b2+b3,c1+c2+c3+c4},{a1,b1+b2,c1+c2+c3+c4},{a1+a2+a3+a4+a5,b1+b2,c1+c2+c3+c4},{a1+a2+a3+a4+a5,b1+b2+b3,c1+c2+c3+c4}},
{{a1+a2,b1,c1+c2},{0,b1,c1+c2},{0,b1+b2,c1+c2},{a1+a2,b1+b2,c1+c2}},
{{a1+a2+a3,b1,c1+c2},{a1+a2,b1,c1+c2},{a1+a2,0,c1+c2},{a1+a2+a3,0,c1+c2}},
{{a1+a2+a3,b1+b2+b3+b4,c1},{a1+a2,b1+b2+b3+b4,c1},{a1+a2,0,c1},{a1+a2+a3,0,c1}},
{{a1+a2+a3,b1+b2+b3+b4,c1+c2+c3+c4+c5},{a1+a2,b1+b2+b3+b4,c1+c2+c3+c4+c5},{a1+a2,b1+b2+b3,c1+c2+c3+c4+c5},{a1+a2+a3,b1+b2+b3,c1+c2+c3+c4+c5}},
{{a1+a2+a3+a4,b1,c1+c2},{a1+a2+a3,b1,c1+c2},{a1+a2+a3,b1+b2+b3+b4+b5,c1+c2},{a1+a2+a3+a4,b1+b2+b3+b4+b5,c1+c2}},
{{a1+a2+a3+a4,b1,c1+c2+c3},{0,b1,c1+c2+c3},{0,b1+b2,c1+c2+c3},{a1+a2+a3+a4,b1+b2,c1+c2+c3}},
{{a1+a2+a3+a4,b1+b2+b3,c1+c2+c3},{a1+a2+a3,b1+b2+b3,c1+c2+c3},{a1+a2+a3,b1+b2+b3+b4+b5,c1+c2+c3},{a1+a2+a3+a4,b1+b2+b3+b4+b5,c1+c2+c3}},
{{a1+a2+a3+a4+a5,b1+b2+b3,c1+c2+c3},{a1+a2+a3+a4+a5,b1+b2,c1+c2+c3},{a1+a2+a3+a4,b1+b2,c1+c2+c3},{a1+a2+a3+a4,b1+b2+b3,c1+c2+c3}}};
Is there a solution with fewer rectangles? Is there a solution that uses an entire set (sans blanks) of domino-based rectangles, such as the 36 in the double-8 set?
Union[Sort /@ Tuples[Range[8], {2}]]