Message Boards Message Boards

Why it's time to embrace matrix products

Bill Gosper, Home
Posted 8 years ago

NOTE: the notebook with Wolfram Language code is attached at the end of the post

enter image description here

It's time to embrace matrix products. They strictly generalize infinite series, products, and continued fractions. Here are two examples where they efficiently represent the Fourier coefficients of fractals which apparently lack the traditional representations. By the way, in response to the this, Robert Fathauer sent the photo below (left) of the objects he apparently makes from porcelain. It is a 3D print that was collaborative work with Henry Segerman and David Bachman. On the right is the image from Robert Fathauer's website.

enter image description here

Example 1

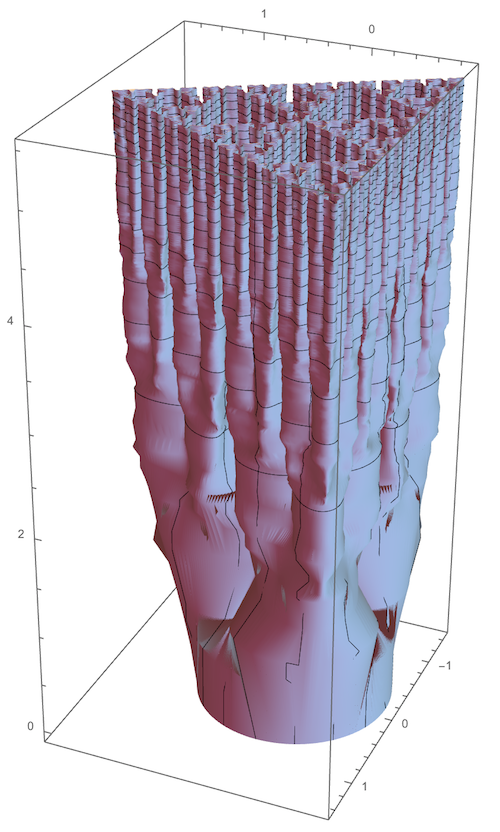
The sweep of the 2D subset of the complex plane representable in the base 2 using the digits 0, 1, and $(-1)^{\pm 2/3}$. This is $2m = six$ Sierpi?ski Gasket sweeps arranged alternately inward and outward around a regular 2m-gon. Found originally as a 3*3 product by Julian Ziegler Hunts. The $Subscript_{1,1}$ indicates the upper left element of the infinite product.

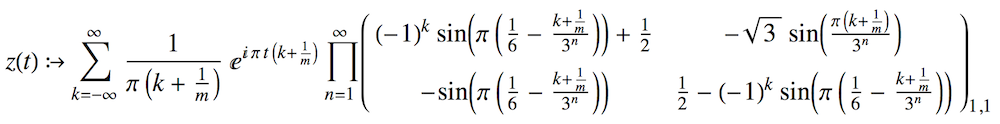
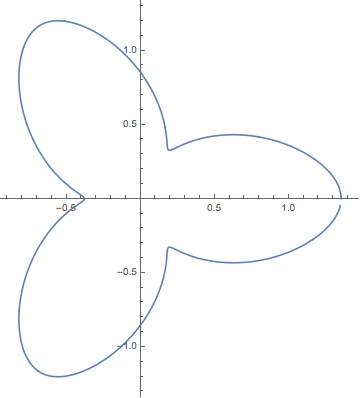
enter image description here

enter image description here

enter image description here

ParametricPlot[{Re[#], Im[#]} &@base2[t, -239, 239], {t, 0, 6}, PlotPoints -> 3^7, Axes -> None]

enter image description here

ParametricPlot3D[{Re[#], Im[#], Log[1 + j]} &@
  base2[t, Ceiling[-j/2], Floor[(j + 1)/2]], {t, 0, 6}, {j, 0, 69}, 
 PlotPoints -> {129, 70}]

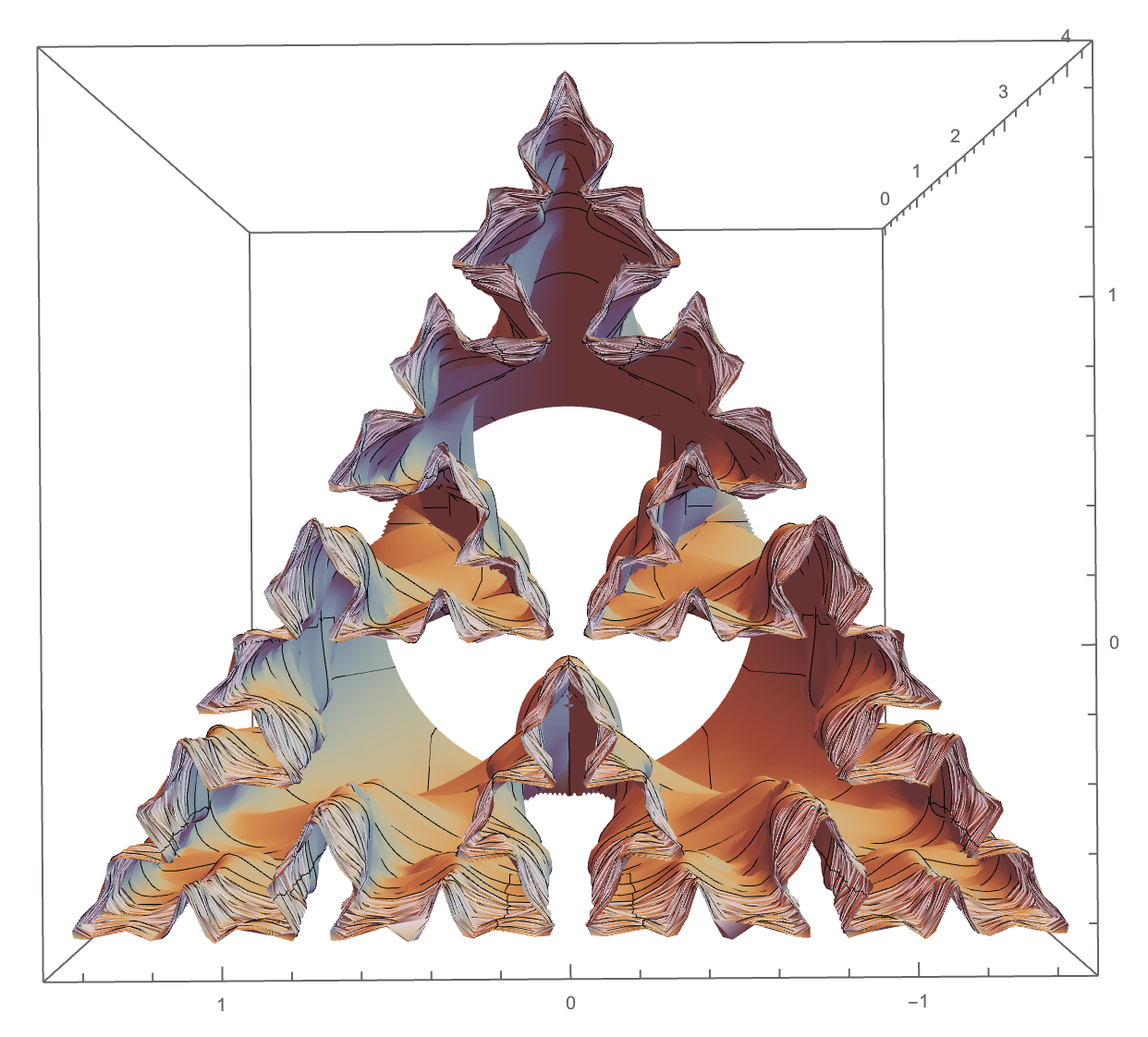
enter image description here

enter image description here

ParametricPlot3D[{Re[#], Im[#], Log[1 + j]} &@
  base2[t, Ceiling[-j/2], Floor[(j + 1)/2]], {t, 0, 6}, {j, 0, 239}, 
 PlotPoints -> {239, 70}]

enter image description here

Example 2

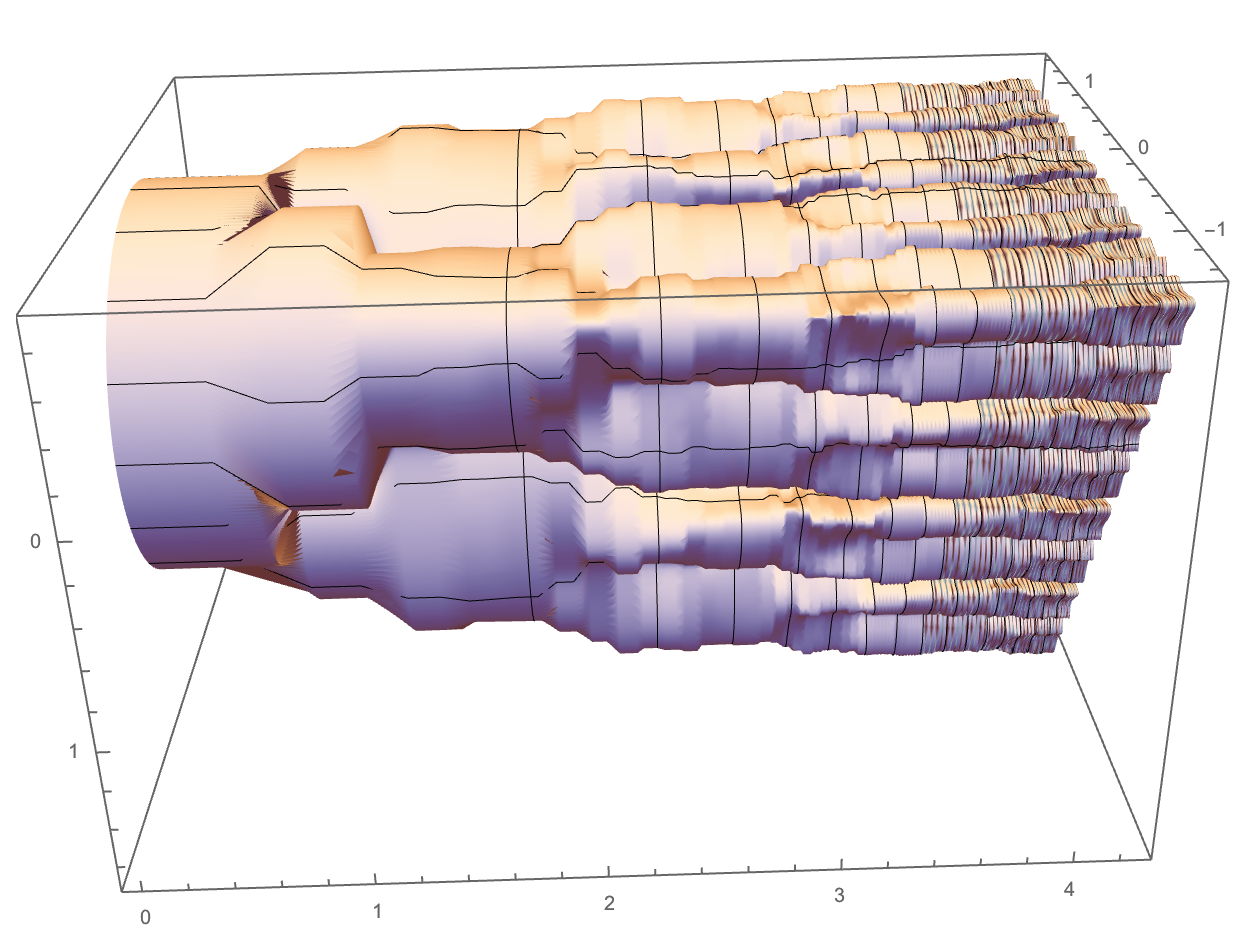
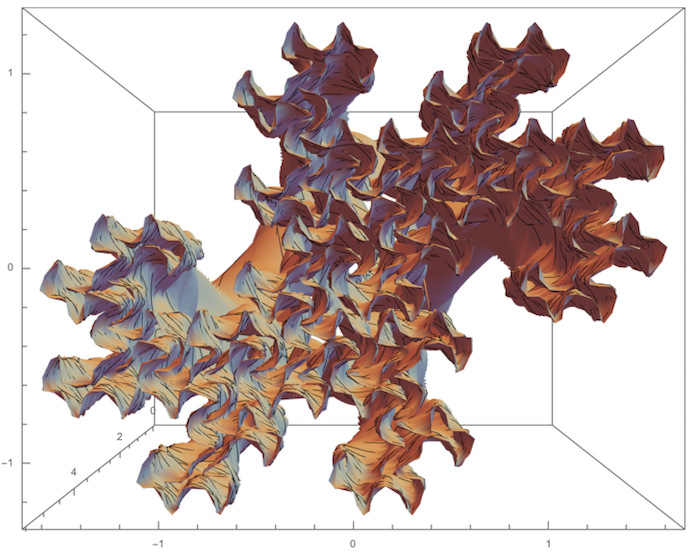
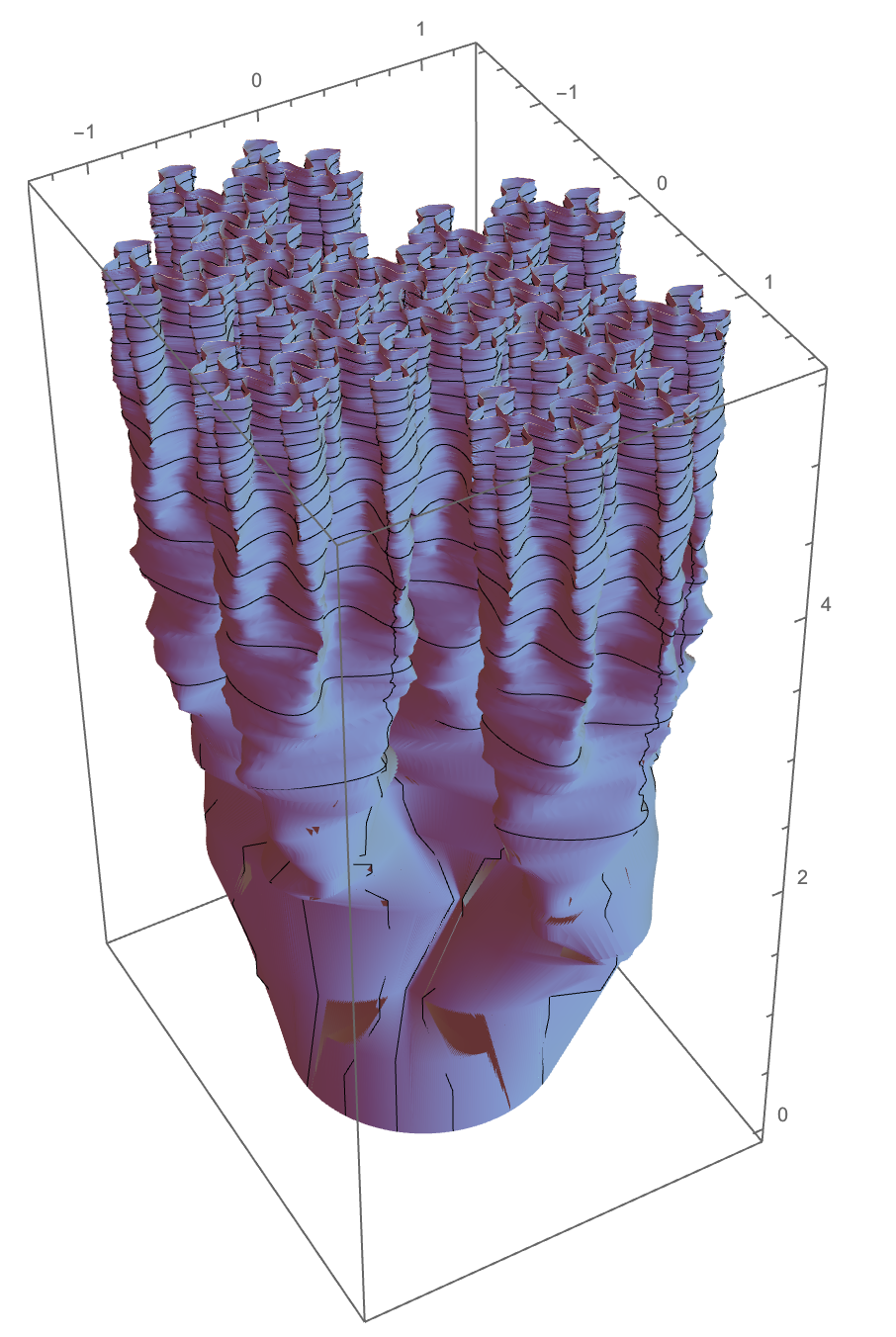
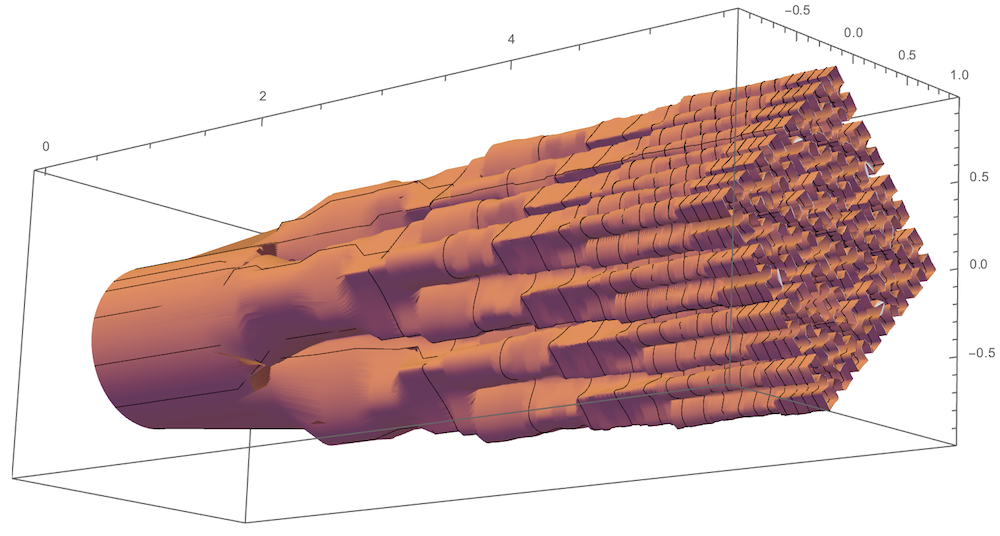
The Twindragon Sweep. $\alpha = half the fold angle = \pi/4$ in the space-filling case. The Twindragon fills the subset of the complex plane representable base i-1 using the digits 0 and 1. The function BProd returns the upper right element of the approximate infinite matrix product.

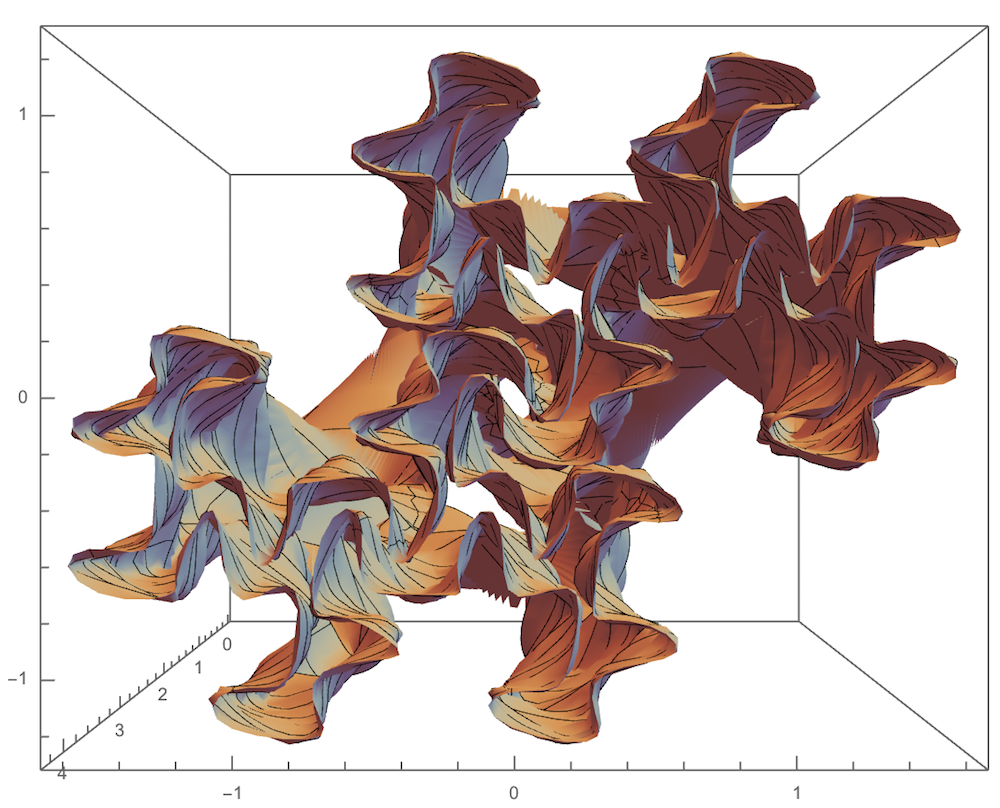
enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

ParametricPlot3D[{Re[#], Im[#], Log[1 + n]} &@
  drag[t, Ceiling[-n/2], Floor[(n + 1)/2]], {t, 0, 4}, {n, 0, 239}, 
 PlotPoints -> {239, 70}]

enter image description here

enter image description here

Example 3 (surprise!)

Here is a 3D print by Neil Bickford of a Fudgeflake Sweep sweep (sic), with a Fourier coefficient derived as a matrix product that happened to telescope to an ordinary product. This m=3 case may be thought of as three Triadic Dragons in a triangular loop.

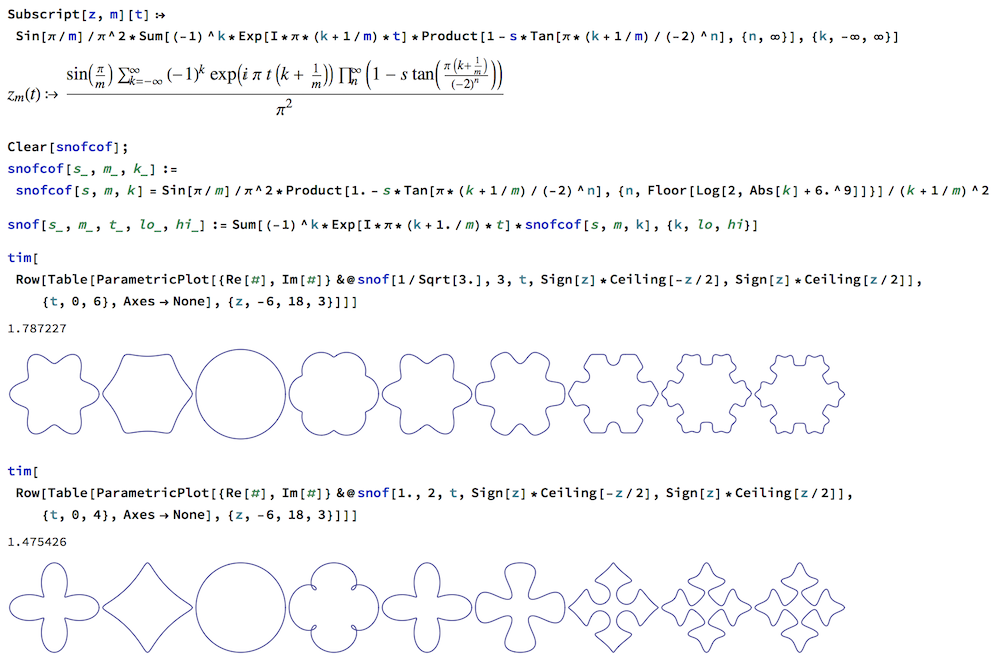
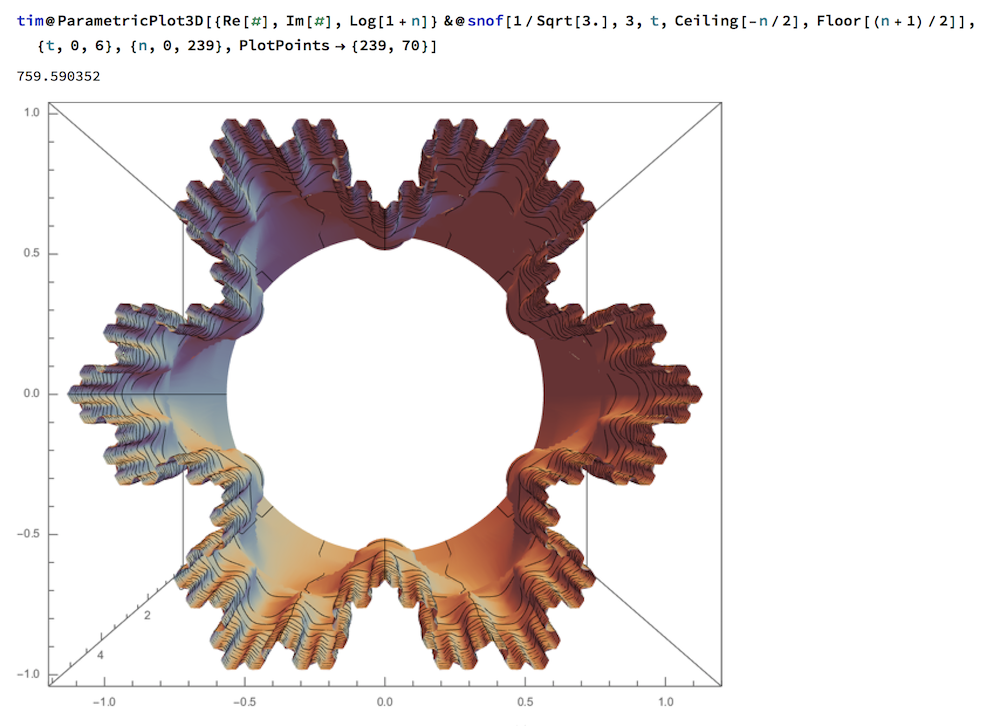
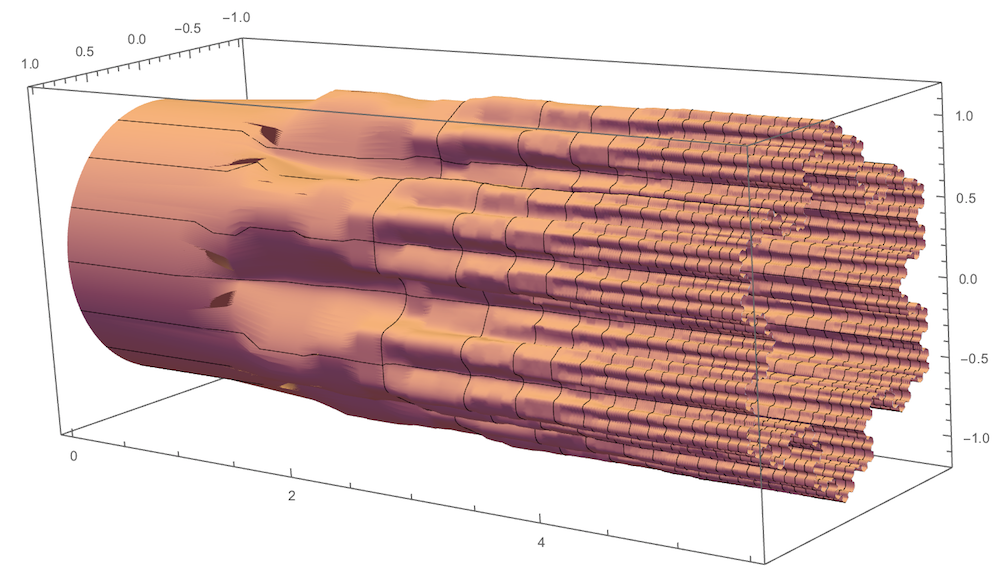
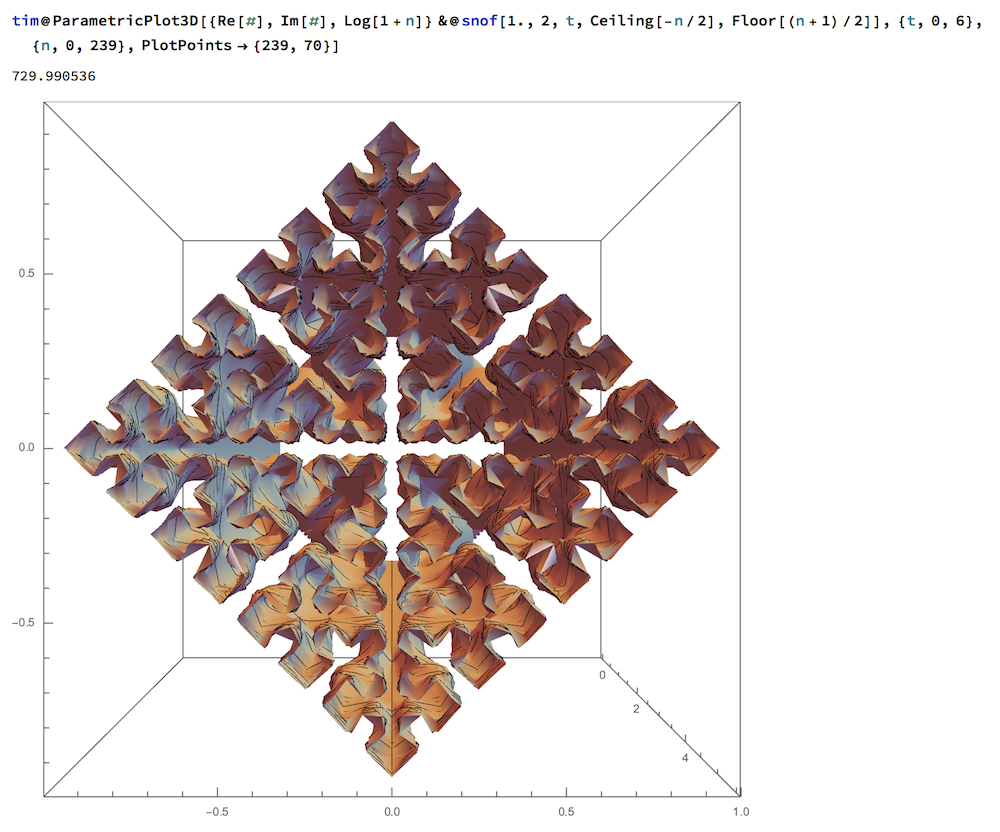
enter image description here

enter image description here

Example 4

As in Example 3, a matrix product telescopes to give the Fourier series for a class of fractals including both the Snowflake curve (m=3, s= 1/Sqrt[3]) and Sierpi?ski's squarefill (m=2, s=1).

enter image description here

enter image description here

enter image description here

enter image description here

enter image description here

Attachments:
POSTED BY: Bill Gosper
4 Replies
Sort By:

The first pics remind me somehow of the behaviour of Fluoroapoatite when crystallized under certain conditions.

http://www.pharmchem.uni-muenchen.de/ac/kluefers/homepage/L/biominerals/apatite7.pdf

The observed features could be simulated by a simple "fractal"-approach, but it would be interesting whether they could be described as well by the principles used here.
POSTED BY: Hans Dolhaine
J. M.
J. M.
Posted 6 years ago

As I had explained in this other post, one can use Array[] to implement (finite sections of) infinite matrix products. For illustration purposes, I will demonstrate with Bill's first example.

gasketProduct[m_Integer?Positive, k_Integer, prec_: MachinePrecision] := 
      Array[Function[n, N[With[{s1 = Sin[? (1/6 - (k + 1/m)/3^n)]},
                               {{1/2 + (-1)^k s1, -Sqrt[3] Sin[? (k + 1/m)/3^n]},
                                {-s1, 1/2 - (-1)^k s1}}], prec]],
            Ceiling[20 + RealExponent[1 + Abs[k], m]], 1, Dot][[1, 1]]

base2cof[m_Integer?Positive, n_Integer?Positive, t_] := 
        Sum[gasketProduct[m, k] Exp[I ? t (k + 1/m)]/(? (k + 1/m)),
            {k, -n, n}, Method -> "Procedural"]

Just to be a little different, I'll use a pentagon as a motif:

ParametricPlot[ReIm[base2cof[5, 30, t]], {t, 0, 4 ?}, PlotPoints -> 105]

pentagonal curvy fractal

ParametricPlot[ReIm[base2cof[5, 120, t]], {t, 0, 4 ?}, MaxRecursion -> 1, PlotPoints -> 905]

even more curvy pentagonal fractal
POSTED BY: J. M.

Bill, these are very pretty, indeed, thank you very much for sharing! Here is another video hosted by Henry's channel: Developing terdragon curve.

enter image description here
POSTED BY: Marina Shchitova

The shapes remind of Space-Filling Curves - Numberphile. Look half-way or so, very similar stuff! Very nicely done!

enter image description here
POSTED BY: Sander Huisman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract