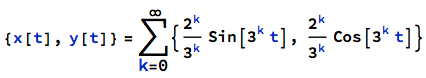
I call it a Weierstrass fractal because it resembles the Weierstrass Function: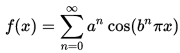

plaht[d_] := ParametricPlot[
  Sum[If[Floor[d] == k, FractionalPart[d], 
     1] {(2/3)^k Sin[3^k t], (2/3)^k Cos[3^k t]}, {k, 0, Floor[d]}]
  , {t, 0, 2 Pi}, PlotRange -> {{-2.2, 2.2}, {-3, 3}}, Axes -> False, 
  PlotPoints -> 50 + Floor[d^5.03], MaxRecursion -> 5, 
  PlotStyle -> {Thickness[
     Piecewise[{{0.015 - (0.0135 d)/8, 
        d < 8}, {0.0015 + 0.00144 (0.04 (d - 13)^2 - 1), d >= 8}}]], 
    Cyan}, Background -> GrayLevel[0.4 (13 - d)/13], 
  ImageSize -> {400, Automatic}]

Export the frames (to make the GIF):

Do[Export[StringJoin[ToString[i, InputForm], ".png"], plaht[i/30]], {i, 0, 390, 1}]

Play with it:

Manipulate[plaht[d],{d,0,13}]