Take a strip of 7 triangles, tape the edges of the end triangles together, and fold it to make an octahedron.

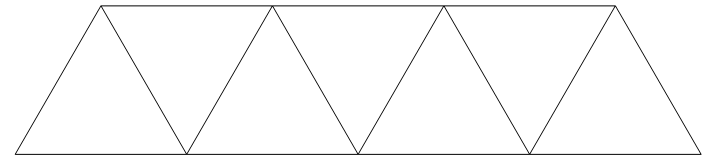
Row[Table[Graphics[{ Line[{ {Sqrt[3], 1}, {0, 2}, {Sqrt[3], 3}, {0, 4}, {Sqrt[3], 5}, {0, 6}, {Sqrt[3], 7}, {0, 8}, {0, 0}, {Sqrt[3], 1}, {Sqrt[3], 7} }]}, ImageSize -> {173, 800} .9], {4}]]

Consider the following set of points:

triloop2 = {{{6, 2, 2}, {5, 1, 6}, {6, 5, 5}}, {{6, 2, 2}, {3, 2, 5}, {6, 5, 5}}, {{3, 2, 5}, {3, 5, 2}, {6, 2, 2}}, {{2, 1, 3}, {6, 2, 2}, {3, 5, 2}}, {{2, 4, 6}, {3, 5, 2}, {2, 1, 3}}, {{5, 1, 6}, {2, 4, 6}, {2, 1, 3}}, {{5, 1, 6}, {2, 4, 6}, {6, 5, 5} }};  
triloop4 = {{{9, 39, 12}, {18, 48, 30}, {12, 24, 36}}, {{9, 39, 12}, {29, 41, 22}, {12, 24, 36}}, {{29, 41, 22}, {27, 21, 12}, {9, 39, 12}}, {{33, 45, 6}, {9, 39, 12}, {27, 21, 12}}, {{36, 30, 30}, {27, 21, 12}, {33, 45, 6}}, {{18, 48, 30}, {36, 30, 30}, {33, 45, 6}}, {{18, 48, 30}, {36, 30, 30}, {12, 24, 36}}}/6;

That set of triangles gives the solution. It's a combination of an octahedron and a tetrahedron. The tetrahedron point touches the center of the opposite point.

Graphics3D[{ Polygon /@ triloop2}, SphericalRegion -> True, Boxed -> False, ImageSize -> {600, 600}] 

Curiously, two of these can be put together so that the bottom triangles have edge to edge contact.

Graphics3D[{ Polygon /@ triloop2, Polygon /@ triloop4}, 
 SphericalRegion -> True, Boxed -> False, ImageSize -> {600, 600}]