The original idea of this article is from my primitive trial to solve
Problem 143 of Project Euler. I am not presenting a solution to this problem, instead, I want to demonstrate how to easily launch multiple threads from compiled code without using extra licenses.
Briefly speaking, I am looking for the triangle ABC with interger sides AB = c, BC= a and CA = b , provided that the distances between the
first Fermat Point of this triangle and its vertices are integers (distances are denoted as p, q and r) and the sum p+q+r is preset with value s, as well. Finally I will sum up all distinct values of s under 120,000 which yields at least one integer tuple (a, b, c, p, q, r) .
Here is my code:
Because
Compile[] only supports a limited number of Mathematica function, I need to define some internal function by myself. For instance, IntegerQ[Sqrt[<An Integer>]] will not work in the compiled code as the
IntegerQ cannot be compiled. So this perfect square check function is rewrote in simple functions:
perfectSquareQ =
Compile[{{n, _Integer}},
Module[{sq = Floor[Sqrt[Abs[n]]]}, If[sq^2 == n, True, False]]]
I can quickly check this function as Compile returns an functional object which is very similar to
LinearModelFit In[1]:= perfectSquareQ[5]
Out[1]:= False
Then comes the main body of the procedure. I use "cf" to denote my compiled function. This "cf" basically checks if a given integer sum p+q+r can produce integer sides of a trianle. There may be multiple results or no result. "cf" terminates either when it finds the first solution or after it scans every possibilities in vain (a costly situation).
cf = Compile[{{limit, _Integer}},
Module[{limP = Ceiling[limit/3], r = 1, a = 0, b = 0, c = 0,
res = 0},
Do[
If[res > 0, Break[]];
Do[
r = limit - p - q;
a = Abs[(limit - p)^2 - r*q];
b = Abs[(limit - r)^2 - p*q];
c = Abs[(limit - q)^2 - p*r];
(*If[b>510,Print[{a,b}]];*)
If[perfectSquareQ[a] && perfectSquareQ[b] && perfectSquareQ[c],
res = limit; Break[]]
, {q, Ceiling[(limit - p)/2], limit - p - 1}]
, {p, limit - 2, limP, -1}];
res
],
CompilationTarget -> "C",
CompilationOptions -> {"InlineExternalDefinitions" -> True},
RuntimeAttributes -> {Listable},
Parallelization -> True
]
Besides the function code itself, you can see I have several options in the definition of "cf".
- CompilationTarget: This option tells Mathematica to use the compiled C code instead of runing with "WVM" (wolfram virtual machine)
- CompilationOptions: I use this option because the "cf" calls another compile function "perfectSquareQ"
- RuntimeAttributes/Parallelization: These two options are critical to our parallel computation process. The symbol RuntimeAttributes is similar to SetAttributes, here it let the head "cf" take elements of a list automatically, ie. cf[{1,2,3}] -> {cf[1],cf[2],cf[3]}. While Parallelization let cf[1] , cf[2] and cf[3] get executed on different cpu cores automatically. With these two options, cf[Range[1,100]] can be parallelized with no effort.
As you run this code on your machine (with proper C compiler), you can see check the following statistics from the system monitor:
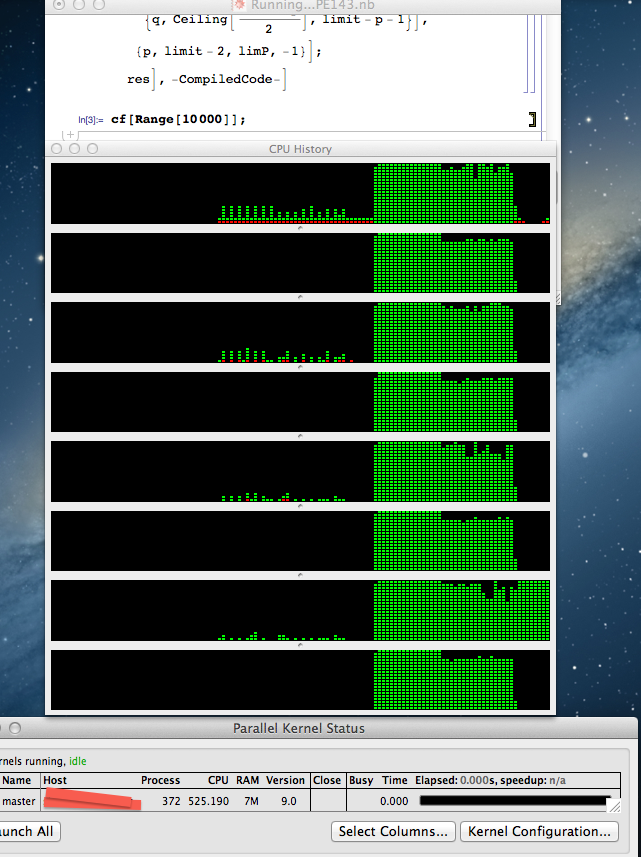
Of course this method still takes a rather long time to find the possibilites of p+q+r < 30,000 if you do not adopt a smart algorithm with number theory thinges. However, you may save a lot of time to do similar procedure programmings with many jumpy cases, which are not suitable for
Map or
Table function in Mathematica.