The result I am expecting does not extend to the imaginary numbers. I perhaps should have given some back ground info, my mistake. In this context just strict the Domain/ Range to real numbers. What I was looking for was just a solution to a seperable differential equation, which would give me a velocity-time graph until the terminal velocity is reached. Anyways I managed to do the plot using another application. And I took the inverse of the function using a pen lol. Also in this context {a,b,c} are variables independant of x. For instance "c" is the mass of a skydiver. The initial reason why I used Alpha was that I did not want to lose time with basic calculations. I knew the physics behind the phenomenon so I recognized that the result I received was impossible to obtain and was wrong. And of course you are right about restricting domains when using tan(x), however unlike tan(x): tanh is invertible for the whole domain it is defined on. Of course this is with real numbers only, ( I dont really know how its extension on the complex plane looks like) but the taylor series expansion of tanh(x) can possibly be used to get an idea... Though I am not sure, just guessing.
In the end It just surprized me that Wolfram Alpha failed to comply an algorithm even GeoGebra could comply. What i was trying to obtain was as simple as that. By the way the plot of that inverse function which started this in the first place is as follows where constants {a,b,c} are put in place. y axis represents the horizontal velocity, x axis represents time.
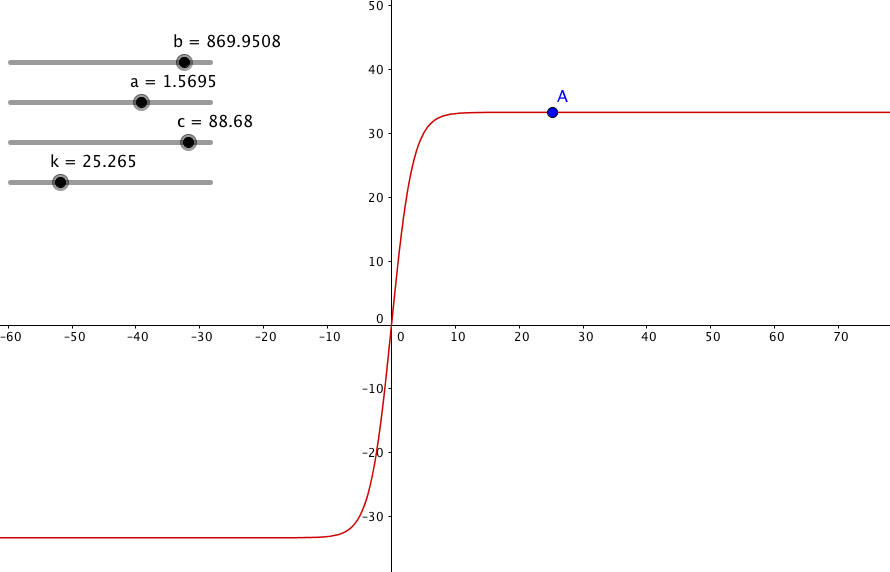
Finally and off the topic as well I didn't really understand what you meant by saying i^1,i^2,i^3,i^4 are not imaginary, could you explain it a little further. Because I thought that everything we know in current mathematics is actually defined under the complex numbers. you caught my attention.