@Yahia,
You may want to simplify the equation first. Usually wrapping a Log function is a good idea here on the both sides of this equation. However, Mathematica will not convert Log [a b] to Log + Log [ b]
since the latter contains more leaf count. We can use a repeated replace function to expand the logrithm function:
In[6]:= Log[(2*(m)^m)/Gamma[m]*(1/2)^((2 m - 1)/n)*E^(-m (1/2)^(2/n))] //.
{Log[x_*y_] :> Log[x] + Log[y], Log[x_/y_] :> Log[x] - Log[y], Log[x_^y_] :> y*Log[x]}
Out[6]= -2^(-2/n) m + (1 - (-1 + 2 m)/n) Log[2] + m Log[m] - Log[Gamma[m]]
Then you can numerically solve the Out[6] with a given "n":
In[19]:= n = 1; FindRoot[-2^(-2/n) m + (1 - (-1 + 2 m)/n) Log[2] + m Log[m] - Log[Gamma[m]] == Log[0.778], {m, 1}]
Out[20]= {m -> 1.01603}
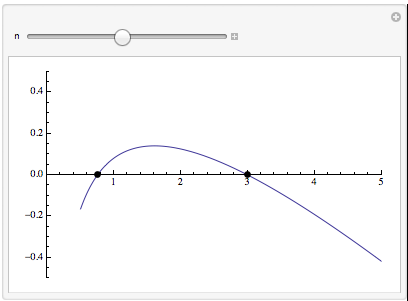
If you want to check the number of the real roots, you may plot this function. For some of values of "n" there are actually two real roots, which I found graphically. Finally, to test the behavior of the roots of this equation, you cannot find a better solution without using Manipulate function:
Manipulate[
sol = FindRoot[-2^(-2/n) m + (1 - (-1 + 2 m)/n) Log[2] + m Log[m] -
Log[Gamma[m]] == Log[0.778], {m, 1}];
sol2 = FindRoot[-2^(-2/n) m + (1 - (-1 + 2 m)/n) Log[2] + m Log[m] -
Log[Gamma[m]] == Log[0.778], {m, 5}];
Plot[-2^(-2/n) m + (1 - (-1 + 2 m)/n) Log[2] + m Log[m] -
Log[Gamma[m]] - Log[0.778], {m, 0.5, 5},
PlotRange -> {{0, 5}, {-0.5, 0.5}},
Epilog -> {PointSize[0.02], Point[{m, 0} /. sol[[1]]],
Point[{m, 0} /. sol2[[1]]]}]
, {n, 1.2, 1.72}]