Group Abstract Group Abstract

Message Boards Message Boards

0
|
12.7K Views
|
7 Replies
|
7 Total Likes
View groups...
Share
Share this post:

Calculate the sum of an infinite series?

I have two convergent series. Their convergence is testable in Mathematica:

In[1]:= SumConvergence[1/Sqrt[n] - Sqrt[Log[1 + 1/n]], n]

Out[1]= True

In[4]:= SumConvergence[1/Sqrt[n] Log[1 + 2/(n - 1)], n]

Out[4]= True

Unfortunately, Mathematica doesn't find their sums, at least on my computer and system:

In[6]:= Sum[1/Sqrt[n] - Sqrt[Log[1 + 1/n]], {n, \[Infinity]}]

Out[6]= \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n\), \(\[Infinity]\)]\((
\*FractionBox[\(1\), 
SqrtBox[\(n\)]] - 
\*SqrtBox[\(Log[1 + 
\*FractionBox[\(1\), \(n\)]]\)])\)\)

In[5]:= Sum[1/Sqrt[n] Log[1 + 2/(n - 1)], {n, 2, \[Infinity]}]

Out[5]= \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = 2\), \(\[Infinity]\)]
\*FractionBox[\(Log[1 + 
\*FractionBox[\(2\), \(\(-1\) + n\)]]\), 
SqrtBox[\(n\)]]\)

Can someone find the sums and help to exclude the trouble?
POSTED BY: Valeriu Ungureanu
7 Replies
Sort By:

Every term is bounded by -1/(k(k+1)) and 1/(k(k+1)), these both converge to -1 and 1 respectively. I think one can then safely assume that the Sin[...]/(k(k+1)) also always converges.
POSTED BY: Sander Huisman

Another infinite series for which I can't verify the convergence...

SumConvergence[Sin[k!]/(k (k + 1)), k, 
 Method -> {"RatioTest", "RootTest", "RaabeTest", "IntegralTest"}]

I can calculate the approximate value of the sum with NSum[] with machine precision:

In[57]:= SumConvergence[Sin[k!]/(k (k + 1)), k, 
 Method -> {"RatioTest", "RootTest", "RaabeTest", "IntegralTest"}]

In[63]:= NSum[Sin[k!]/(k (k + 1)), {k, 1, \[Infinity]}]

During evaluation of In[63]:= NIntegrate::slwcon: Numerical integration converging too slowly; suspect one of the following: singularity, value of the integration is 0, highly oscillatory integrand, or WorkingPrecision too small.

During evaluation of In[63]:= NIntegrate::ncvb: NIntegrate failed to converge to prescribed accuracy after 9 recursive bisections in k near {k} = {45.385}. NIntegrate obtained -0.00397379 and 0.003836148173776894` for the integral and error estimates.

During evaluation of In[63]:= NSum::emcon: Euler-Maclaurin sum failed to converge to requested error tolerance.

Out[63]= 0.541556

We can define a function that may be used to "visualize" the behavior of partial sums:

f[n_] := Sum[Sin[k!]/(k (k + 1)), {k, 1, n}]

Plot[f[n], {n, 1, 33}, PlotRange -> {{0, 33}, {0.2, 0.72}}]

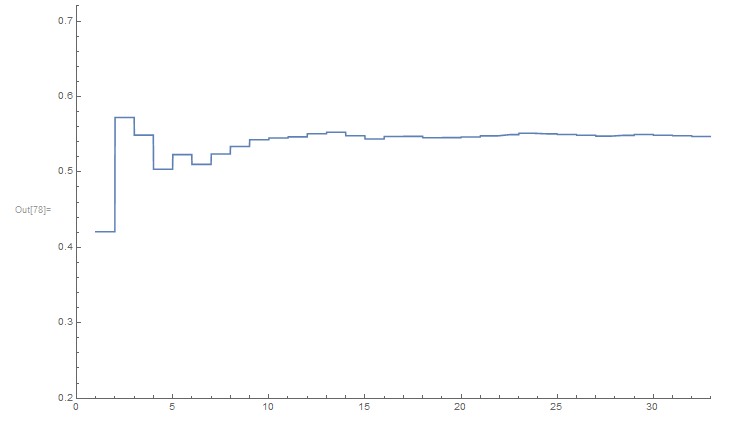
enter image description here

It seems that the series is convergent. We can refer the "policemen" rule in this context. But, can we test simply in Mathematica the convergence of this series?

Can we compute the sum with a greater precision and accuracy?
POSTED BY: Valeriu Ungureanu

Evidently, it doesn't evaluate for n = 0 because of dividing to 0...
POSTED BY: Valeriu Ungureanu

The only way I can make it give an (reasonable) answer, without giving an error is as follows:

NSum[1/Sqrt[n] - Sqrt[Log[1 + 1/n]], {n, 1, Infinity}, 
 Method -> {"EulerMaclaurin", 
   Method -> {"NIntegrate", Method -> "LocalAdaptive"}}]

giving the same 0.53...
POSTED BY: Sander Huisman

Even that second one is probably not correct:

NSum[1/Sqrt[n] - Sqrt[Log[1 + 1/n]], {n, 1, Infinity}, WorkingPrecision -> 35]

gives roughly 0.53310...

but it still returns some errors for convergence...
POSTED BY: Sander Huisman
Paul Cleary
Paul Cleary
Posted 9 years ago

If we try

NSum[1/Sqrt[n] - Sqrt[Log[1 + 1/n]], {n, 0, Infinity}]

It won't evaluate, but

NSum[1/Sqrt[n] - Sqrt[Log[1 + 1/n]], {n, 1, Infinity}]

1.96429*10^123
POSTED BY: Paul Cleary

That a sum converges does not necessarily mean that its sum can be written as a 'nice' constant. I think this is such a case:

NSum[1/Sqrt[n] Log[1 + 2/(n - 1)], {n, 2, \[Infinity]}]

gives 3.32138.

I'm not so sure about the first one though... even NSum seems to find something that blows up. I think it is the Raabe test that gives True. But I can't comment if that always works or if another kind of test is needed.
POSTED BY: Sander Huisman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard