At the Wolfram Demonstrations Project, Mondrian Art Problem is getting some attention. Getting more attention, with almost 2 million views, is the Numberphile video on the Mondrian Puzzle. The links discuss dissecting a square into non-congruent rectangles so that the difference between largest and smallest is minimized. If non-integer rectangles are allowed, a Blanche dissection is possible. It's an open question for whether there is a Blanche dissection with integer rectangles. At the video site, there are many questions and suppositions about the 0 case. There is also a Mondrian video blog which features some of my ramblings as I tried to assist with a tight turn-around.
A side 360 square might be divisible into 8, 9, 10, or 12 non-congruent rectangles. A side 840 square might split into 8, 9, 10, 12, 14, 15, 16, or 20 non-congruent rectangles. The 360 is unlikely, since I used the code at Blanche dissection to look at the 8 to 12 edge graphs corresponding to the 8-12 rectangle solutions. But there are too many 20-edge graphs to check and my program slows down for those cases.
Here's a try at dividing the 360 square into 12 rectangles of the same area. There is an overlap of area 4050, which matches the uncovered area in yellow. Not shown is a 360x30 rectangle which may be substituted for one of the rectangles shown below.
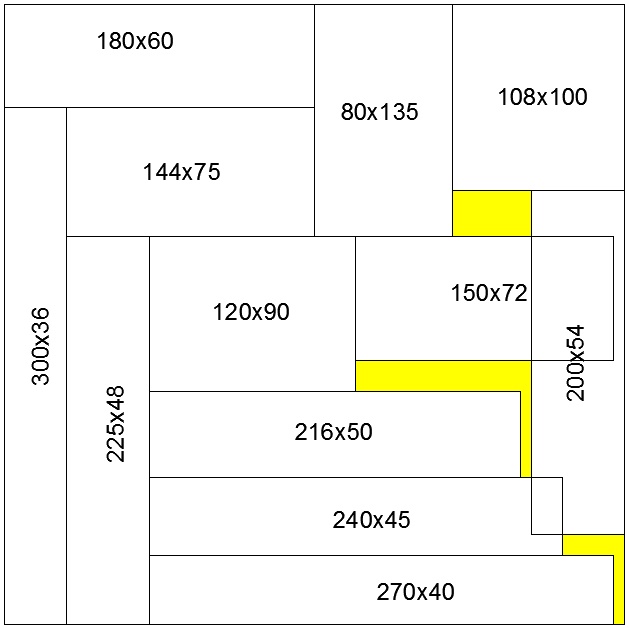
If 12 non-congruent integer-sided rectangles of area 10800 are placed in a side 360 square, what is the minimal possible overlap? Above, an overlap of 4050 is shown. Can that be improved on? Similarly, here are 22 rectangles. Twenty of them might pack a side 840 square. Currently, 19 of them are in a side 840 square. Add one more. What is the minimal possible overlap?
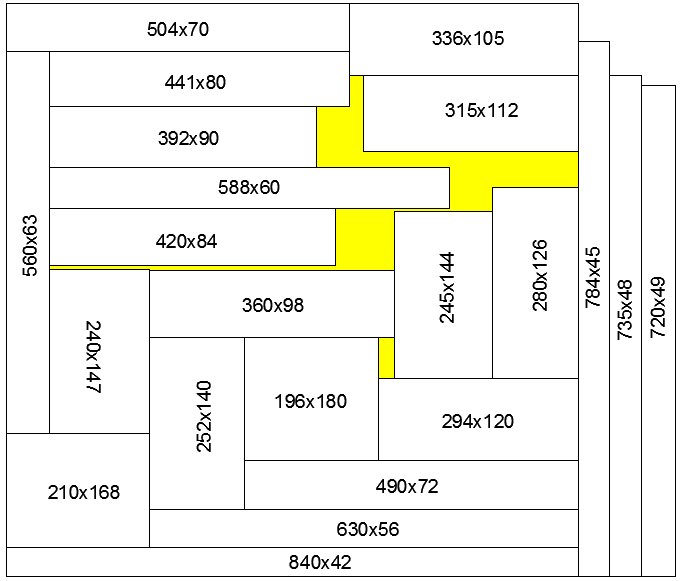
Either of these lines can find the rectangles for the 840 case. Or you can use Rectangles Reasonably Close to a Given Area.
Select[Union[Sort /@ Transpose[{Divisors[840^2 /20], Reverse[Divisors[840^2 /20]]}]], Max[#] <= 840 &]
840 Select[Union[Sort /@ Tuples[Select[Drop[FareySequence[840], 1], IntegerQ[840/Denominator[#]] &], {2}]], Times @@ # == 1/20 &]
I'm working on a new version of the demo that goes up to squares of size 60. I believe I've proven values up to 24, giving the sequence 4, 4, 5, 5, 6, 6, 8, 6, 7, 8, 9, 9, 9, 8, 10, 9, 9, 9, 9, 9, 9, which is tentatively A276523. The proof method is in the new version of the Demonstration. With a known size and defect, it's possible to list all the rectangle sets that might beat it. Then a packing program can try those rectangle sets. I don't have a convenient Mathematica packing program yet, so I used Burr Tools along with a set-up program found here.
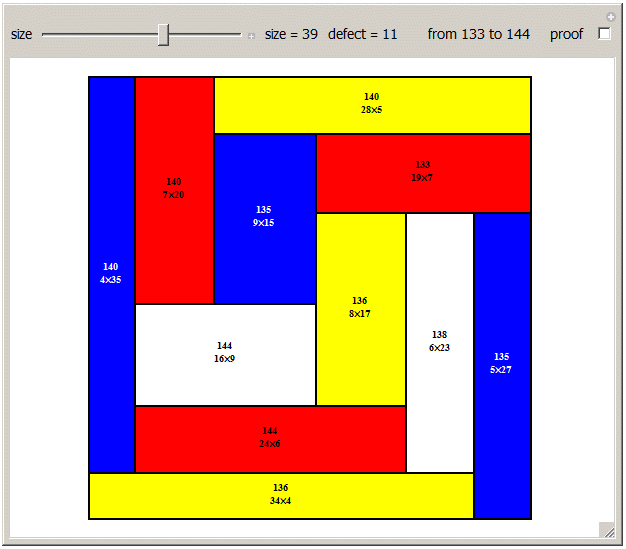
The "proof" part gives a list like the following:
for defect 10 remove 2 with area 190 from the 18 in 90 to 100
for defect 10 remove 5 with area 558 from the 18 in 110 to 120
for defect 9 remove 3 with area 338 from the 16 in 111 to 120
for defect 10 remove 4 with area 459 from the 17 in 111 to 121
for defect 8 remove 2 with area 227 from the 15 in 112 to 120
for defect 9 remove 3 with area 348 from the 16 in 112 to 121
The graph-based Blanche dissection method currently only considers 3-connected graphs, but it's possible for a solution to be based on a 2-connected graph. I need to adapt my program to planar 2-connected graphs with no minimal valence.
The graph method, the numerical method, and the packing method all bog down for larger cases.
I've also looked at the 3rd dimension. For the 6x6x6 case, volumes 12 to 24 work. The solution is unique. Dario Uri made a lovely set for me, just for finding this.

I think the defect for 12x12x12 might be 18, with cuboids of volume 66 to 81. The packing search needs 3 months, and I'm 1.4 months into it. I'm not sure how to translate the 3D problem into something like a graph.
 Attachments:
Attachments: