According to legend, when Hippasus proved the irrationality of $\sqrt2$, he was thrown off a ship. Poor guy.
..
Gauss discovered that the numbers 1, 2, 3, 7, 11, 19, 43, 67, 163 led to unique factorization domains, and conjectured these were the only such numbers. Another person almost forgotten was Kurt Heegner, who proved Gauss's conjecture. But there was a small gap in his proof. Years later, Alan Baker and Harold Stark proved the result. But then they looked at Heegner's proof and announced it was pretty much correct, four years after Heegner's death. In his honor, 1, 2, 3, 7, 11, 19, 43, 67, 163 are known as Heegner numbers.
..
The $\mathbb{Q}(\sqrt{-1})$ numbers are known as Gaussian integers.
The $\mathbb{Q}(\sqrt{-3})$ numbers are known as Eisenstein integers.
The $\mathbb{Q}(\sqrt{-7})$ numbers are known as Kleinian integers.
..
What about $\mathbb{Q}(\sqrt{-2})$? Why doesn't it have a name? I propose we call these Hippasus integers. He doesn't get much credit for his discoveries about $\sqrt{2}$, so may as well give him this to fill in the gap.
..
So what do the Hippasus primes look like? Here's some code based on the Sieve of Eratosthenes that seems to work. I'm sure it can be vastly improved upon.
heeg = 2;
klein = RootReduce[Select[SortBy[Flatten[Table[a + b (Sqrt[heeg] I - 1)/2, {a, -50, 50}, {b, -70, 70}]], N[Norm[#]] &], 1 < Norm[#] < 40 &]];
sieve = Take[#, -2] & /@ (Last /@ (Sort /@ SplitBy[SortBy[{Norm[#]^2, 2 Re[#], 2 Im[#]/Sqrt[heeg]} & /@ klein, Abs[#] &], Abs[#] &]));
primes = {};
Module[{addedprime, remove},
While[Length[sieve] > 1,
addedprime = sieve[[1]];
primes = Append[primes, addedprime];
remove = Union[Join[Abs[{#[[1]], #[[2]]/Sqrt[heeg]}] & /@ (ReIm[2 (addedprime.{1, Sqrt[heeg] I}/2) (#.{1, Sqrt[heeg] I}/2)] & /@ sieve),
Abs[{#[[1]], #[[2]]/Sqrt[heeg]}] & /@ (ReIm[2 (addedprime.{1, -Sqrt[heeg] I}/2) (#.{1, Sqrt[heeg] I}/2)] & /@ sieve)]];
sieve = Select[Drop[sieve, 1], Not[MemberQ[remove, #]] &]]];
Graphics[Table[Point[{{1, 1}, {1, -1}, {-1, 1}, {-1, -1}}[[k]] ReIm[#]] & /@ (#.{1, Sqrt[heeg] I}/2 & /@ primes), {k, 1, 4}]]
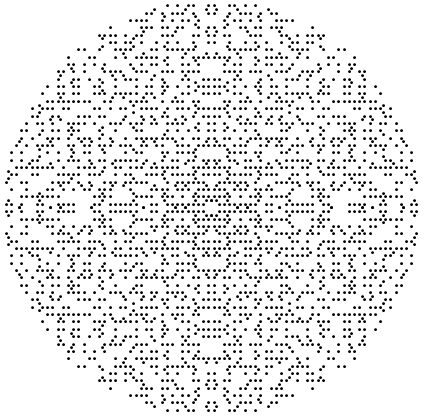
With a change of the Heegner number at the top, the Gaussian primes, Hippasus primes, Eisenstein primes, and Kleinian primes can all be calculated:
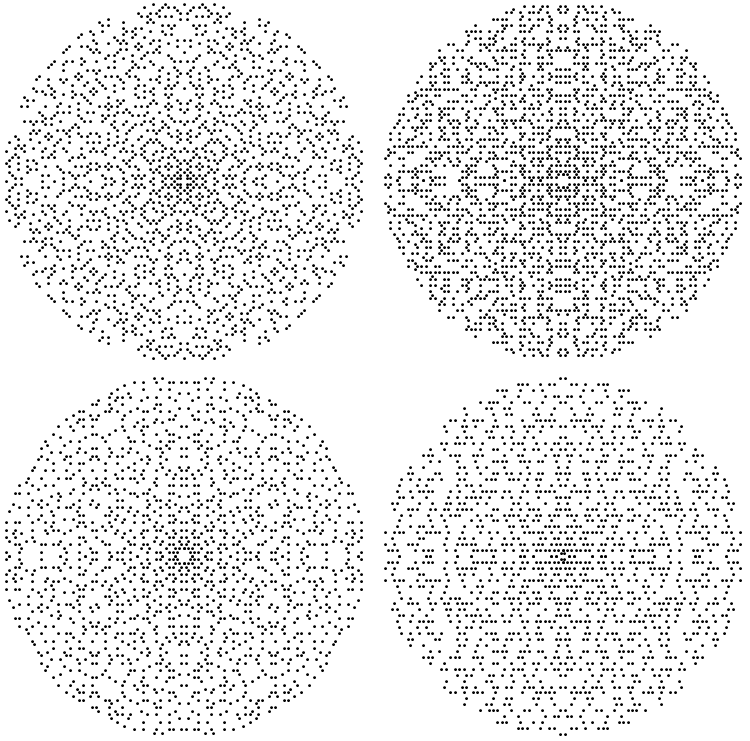
In case you were curious, we can also calculate the primes based on Heegner numbers 11, 19, 43, and 67.
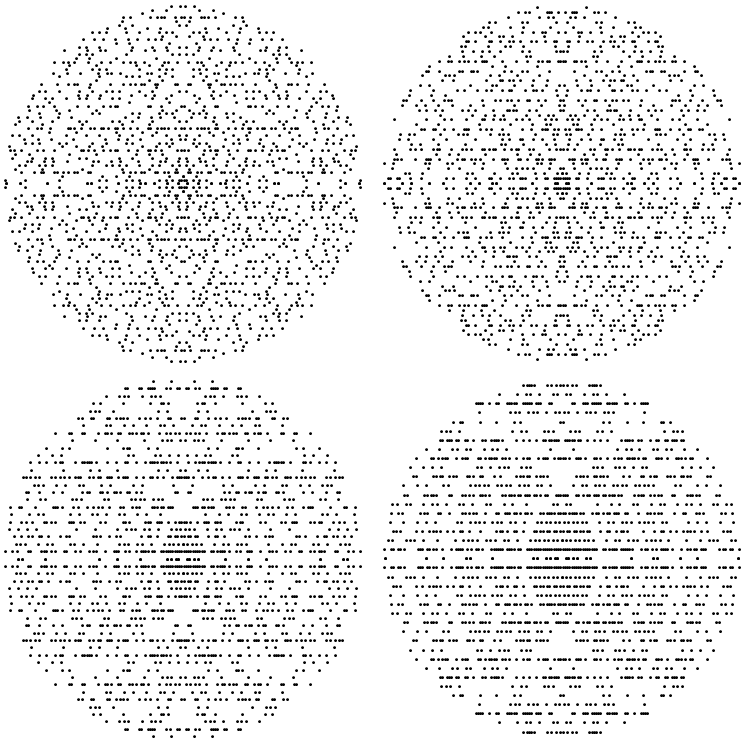
Those last two look pretty weird, so maybe I'm making a mistake somewhere. The primes based on 163 look even stranger.

There are so many weird patterns that I almost didn't show this one. But then I remembered the lucky numbers of Euler, which are based on Heegner numbers. The long line of primes is likely accurate. If anyone can improve/speed up the code and make a much larger picture, I'd love to see that.
..
The same goes for a bigger picture of the Hippasus primes. If there is another name for these, please let me know. If you agree this is a great name for them, also let me know.