Any suggestions on what I can replace CirclePoints and Association with? They are also mathematica 10 commands. I guess I really do need to hassle the IT department for an upgrade.

And Association can be avoided by replacing the two consecutive lines as follows:

lines = Thread[numbers -> pos];
lines = Map[# /. lines &, sol, {2}];

SelectFirst

Was introduced in version 10. So that explains it. You can replace it indeed by the code you mentioned or define a SelectFirst yourself... note that the built-in is a bit more efficient; it will stop 'selecting' after finding the first one, where as yours will 'select' all of them first...

Good luck

I further updated the code to be more smart for large n:

$HistoryLength = 1;
ClearAll[DividePerfectSquarePairs, DividePerfectSquarePairsRecurse, SquareQ, PureQ, VisualizePairs]
SquareQ[n_Integer] := SquareQ[n] = IntegerQ[Sqrt[n]]
PureQ[l_List] := (l === Range[1, Length[l]])
DividePerfectSquarePairsRecurse[pairs_List, left_List] := Module[{cand, n, t, newpairs},
  If[PureQ[left] \[And] Length[left] >= 62,
   n = Length[left];
   t = SelectFirst[Range[n], SquareQ[# + n] \[And] OddQ[#] \[And] # >= 25 &];
   newpairs = {Range[t, t + ((n - t) - 1)/2], Reverse@Range[t + ((n - t) - 1)/2 + 1, n]};
   DividePerfectSquarePairsRecurse[Join[Transpose[newpairs], pairs], Range[t - 1]]
   ,
   If[Length[left] > 2,
    Do[cand = {left[[1]], left[[i]]};
     If[SquareQ[Total[cand]],
      DividePerfectSquarePairsRecurse[Append[pairs, cand], 
       Delete[left, {{1}, {i}}]]
      ]
     ,
     {i, 2, Length[left]}
     ]
    ,
    If[SquareQ[Total[left]],
     Throw[Append[pairs, left]];
     ]
    ]
   ]
  ]
DividePerfectSquarePairs[n_Integer?EvenQ] := Module[{},
  If[SquareQ[n + 1],
   Transpose[{Range[1, n/2], Range[n, n/2 + 1, -1]}]
   ,
   Catch[DividePerfectSquarePairsRecurse[{}, Range[n]]; Missing[]]
   ]
  ]
DividePerfectSquarePairs[n_Integer?OddQ] := Missing[]
VisualizePairs[sol : {{_Integer, _Integer} ..}] := 
 Module[{numbers, len, pos, angles, txts, lines, colors},
  numbers = Union @@ sol;
  colors = ColorData[109] /@ (Sqrt[Total[sol, {2}]] - 1);
  len = Length[numbers];
  pos = Reverse[CirclePoints[{0.0, 0.0}, {1.5, \[Pi]/2 + \[Pi]/len}, len]];
  angles = If[#1 < 0, -{##}, {##}] & @@@ pos;
  txts = MapThread[Text[#1, #2, {0, 0}, #3] &, {numbers, pos, angles}];
  lines = Association[Thread[numbers -> pos]];
  lines = Map[lines, sol, {2}];
  lines = 0.9 {#1, {0, 0}, #2} & @@@ lines;
  Graphics[{txts, Thick, Riffle[colors, BezierCurve /@ lines]}, ImageSize -> 300, PlotRange -> 1.6]
 ]

It can now easily handle n=1000 or even much much bigger (for fun I tried 10^6 and it found the solution in ~19 seconds). It does so by finding a low m (but not too low) such that m....a and a+1 ... n can form pairs that form squares. This reduces then the problem from finding a solution for n, to finding a solution for m-1 (because m...n are 'eliminated').

So now one can type in:

VisualizePairs[DividePerfectSquarePairs[250]]

and quickly get the visual:

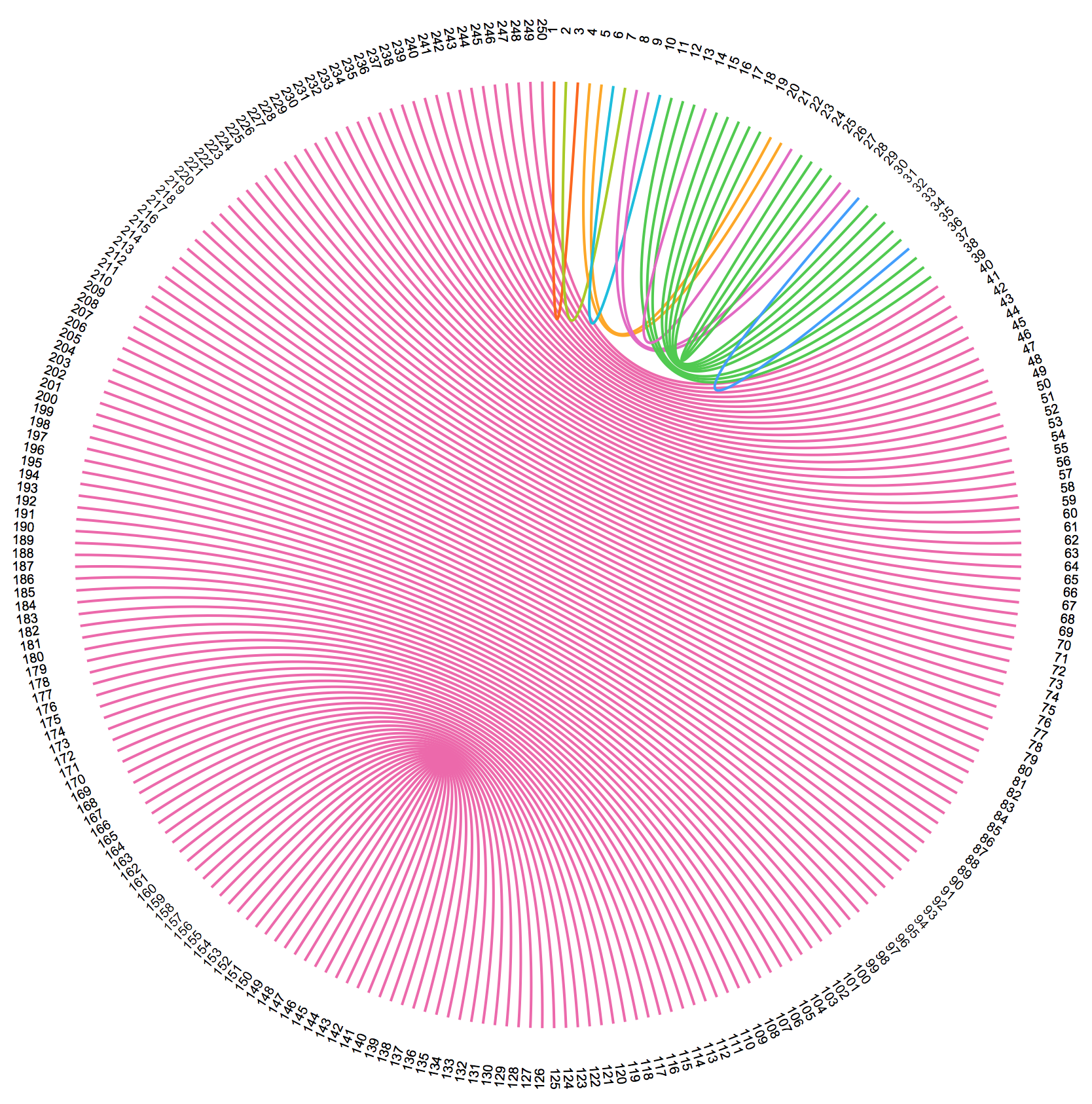
Notice that the problem is quickly reduced to a problem for n = 38. For which we use the old method. One could hard-code the solution for n=2...60 and then this function will be nearly instantaneous for all n (except those that can't be split up).

Dear Ashley,

This is a recursive function that will start with a list of all the integers up to n. This list I call 'left'. From the list 'left' it will pick the first and from the other 2...Length[left] it will pick those that sum up to be square together with the first element. For all those possibilities it will call itself, now with the first argument the good matches, and the remaining digits that are 'left'. If there is nothing left, then we have a solution. I hope you're following my logic, not that easy to explain. This has the advantage that it does not have to compute all possibilities in advance (like permutations and subsets) which takes lots (too much) memory easily. This should be relatively cheap in memory.

$HistoryLength = 1;
ClearAll[DividePerfectSquarePairs, DividePerfectSquarePairsRecurse, SquareQ]
SquareQ[n_Integer] := SquareQ[n] = IntegerQ[Sqrt[n]]
DividePerfectSquarePairsRecurse[pairs_List, left_List] := Module[{cand},
  If[Length[left] > 2,
   Do[
    cand = {left[[1]], left[[i]]};
    If[SquareQ[Total[cand]],
     DividePerfectSquarePairsRecurse[Append[pairs, cand], Delete[left, {{1}, {i}}]]]
    , {i, 2, Length[left]}
    ]
   ,
   If[SquareQ[Total[left]], Throw[Append[pairs, left]];]
   ]
  ]
DividePerfectSquarePairs[n_Integer?EvenQ] := Catch[DividePerfectSquarePairsRecurse[{}, Range[n]]; Missing[]]
DividePerfectSquarePairs[n_Integer?OddQ] := Missing[]

This will recurse through all possibilities and return the first it finds (it can easily be modified to return all possibilities if you want).

DividePerfectSquarePairs[16]
Total /@ %

{{1, 8}, {2, 7}, {3, 6}, {4, 5}, {9, 16}, {10, 15}, {11, 14}, {12, 13}}
{9, 9, 9, 9, 25, 25, 25, 25}

Is it true it can not be done for 2,4, 6, 10, 12, 20, and 22 (and all the odd n of course)?

It can be slightly improved because some of them can be easily solved:

$HistoryLength = 1;
ClearAll[DividePerfectSquarePairs, DividePerfectSquarePairsRecurse, SquareQ]
SquareQ[n_Integer] := SquareQ[n] = IntegerQ[Sqrt[n]]
DividePerfectSquarePairsRecurse[pairs_List, left_List] := Module[{cand},
  If[Length[left] > 2,
   Do[
    cand = {left[[1]], left[[i]]};
    If[SquareQ[Total[cand]],
     DividePerfectSquarePairsRecurse[Append[pairs, cand], Delete[left, {{1}, {i}}]]
     ]
    ,
    {i, 2, Length[left]}
    ]
   ,
   If[SquareQ[Total[left]],
    Throw[Append[pairs, left]];
    ]
   ]
  ]
DividePerfectSquarePairs[n_Integer?EvenQ] := Module[{},
  If[SquareQ[n + 1],
   Transpose[{Range[1, n/2], Range[n, n/2 + 1, -1]}]
   ,
   Catch[DividePerfectSquarePairsRecurse[{}, Range[n]]; Missing[]]
   ]
  ]
DividePerfectSquarePairs[n_Integer?OddQ] := Missing[]

Correct!

How can your method have a solution to 35? The numbers 1..35 can not be divided in two pairs; it is an odd number?

What would the answer for 16 be? If all the pairs have to add up to the same square, at least any odd square minus one would work, so for example the list {1, 2, ..., 24} gives you {{1, 24}, {2, 23}, ..., {12, 13}}, all adding to 25.