What would the answer for 16 be? If all the pairs have to add up to the same square, at least any odd square minus one would work, so for example the list {1, 2, ..., 24} gives you {{1, 24}, {2, 23}, ..., {12, 13}}, all adding to 25.

Something I am doing wrong, since I still have numbers repeated at the beginning of each tuple, please take a look, thanks in advance.

Here is my code

mere[n_Integer] := 
 Module[{perm, squared, novo, rec}, 
  perm = Permutations[Range[n], {2}]; squared = Range[100]^2; 
  novo = Select[perm, #[[1]] < #[[2]] &];
  rec = DeleteCases[If[MemberQ[squared, Total[#]], #] & /@ novo, 
    Null]; Select[rec, Total[#] >= n &]]

See my results

Any help is welcoming ....

How can your method have a solution to 35? The numbers 1..35 can not be divided in two pairs; it is an odd number?

It can be slightly improved because some of them can be easily solved:

$HistoryLength = 1;
ClearAll[DividePerfectSquarePairs, DividePerfectSquarePairsRecurse, SquareQ]
SquareQ[n_Integer] := SquareQ[n] = IntegerQ[Sqrt[n]]
DividePerfectSquarePairsRecurse[pairs_List, left_List] := Module[{cand},
  If[Length[left] > 2,
   Do[
    cand = {left[[1]], left[[i]]};
    If[SquareQ[Total[cand]],
     DividePerfectSquarePairsRecurse[Append[pairs, cand], Delete[left, {{1}, {i}}]]
     ]
    ,
    {i, 2, Length[left]}
    ]
   ,
   If[SquareQ[Total[left]],
    Throw[Append[pairs, left]];
    ]
   ]
  ]
DividePerfectSquarePairs[n_Integer?EvenQ] := Module[{},
  If[SquareQ[n + 1],
   Transpose[{Range[1, n/2], Range[n, n/2 + 1, -1]}]
   ,
   Catch[DividePerfectSquarePairsRecurse[{}, Range[n]]; Missing[]]
   ]
  ]
DividePerfectSquarePairs[n_Integer?OddQ] := Missing[]

Correct!

I further updated the code to be more smart for large n:

$HistoryLength = 1;
ClearAll[DividePerfectSquarePairs, DividePerfectSquarePairsRecurse, SquareQ, PureQ, VisualizePairs]
SquareQ[n_Integer] := SquareQ[n] = IntegerQ[Sqrt[n]]
PureQ[l_List] := (l === Range[1, Length[l]])
DividePerfectSquarePairsRecurse[pairs_List, left_List] := Module[{cand, n, t, newpairs},
  If[PureQ[left] \[And] Length[left] >= 62,
   n = Length[left];
   t = SelectFirst[Range[n], SquareQ[# + n] \[And] OddQ[#] \[And] # >= 25 &];
   newpairs = {Range[t, t + ((n - t) - 1)/2], Reverse@Range[t + ((n - t) - 1)/2 + 1, n]};
   DividePerfectSquarePairsRecurse[Join[Transpose[newpairs], pairs], Range[t - 1]]
   ,
   If[Length[left] > 2,
    Do[cand = {left[[1]], left[[i]]};
     If[SquareQ[Total[cand]],
      DividePerfectSquarePairsRecurse[Append[pairs, cand], 
       Delete[left, {{1}, {i}}]]
      ]
     ,
     {i, 2, Length[left]}
     ]
    ,
    If[SquareQ[Total[left]],
     Throw[Append[pairs, left]];
     ]
    ]
   ]
  ]
DividePerfectSquarePairs[n_Integer?EvenQ] := Module[{},
  If[SquareQ[n + 1],
   Transpose[{Range[1, n/2], Range[n, n/2 + 1, -1]}]
   ,
   Catch[DividePerfectSquarePairsRecurse[{}, Range[n]]; Missing[]]
   ]
  ]
DividePerfectSquarePairs[n_Integer?OddQ] := Missing[]
VisualizePairs[sol : {{_Integer, _Integer} ..}] := 
 Module[{numbers, len, pos, angles, txts, lines, colors},
  numbers = Union @@ sol;
  colors = ColorData[109] /@ (Sqrt[Total[sol, {2}]] - 1);
  len = Length[numbers];
  pos = Reverse[CirclePoints[{0.0, 0.0}, {1.5, \[Pi]/2 + \[Pi]/len}, len]];
  angles = If[#1 < 0, -{##}, {##}] & @@@ pos;
  txts = MapThread[Text[#1, #2, {0, 0}, #3] &, {numbers, pos, angles}];
  lines = Association[Thread[numbers -> pos]];
  lines = Map[lines, sol, {2}];
  lines = 0.9 {#1, {0, 0}, #2} & @@@ lines;
  Graphics[{txts, Thick, Riffle[colors, BezierCurve /@ lines]}, ImageSize -> 300, PlotRange -> 1.6]
 ]

It can now easily handle n=1000 or even much much bigger (for fun I tried 10^6 and it found the solution in ~19 seconds). It does so by finding a low m (but not too low) such that m....a and a+1 ... n can form pairs that form squares. This reduces then the problem from finding a solution for n, to finding a solution for m-1 (because m...n are 'eliminated').

So now one can type in:

VisualizePairs[DividePerfectSquarePairs[250]]

and quickly get the visual:

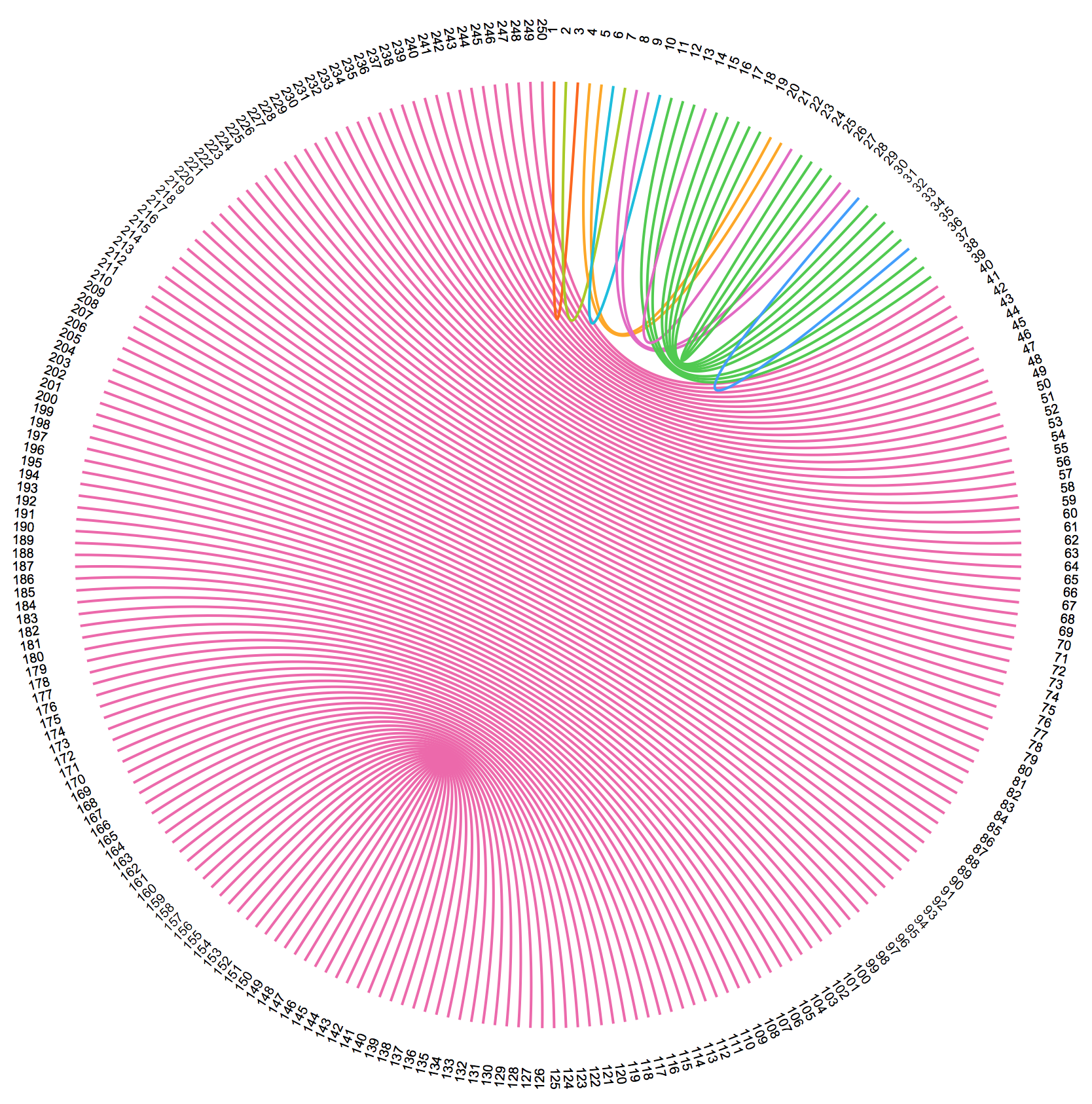
Notice that the problem is quickly reduced to a problem for n = 38. For which we use the old method. One could hard-code the solution for n=2...60 and then this function will be nearly instantaneous for all n (except those that can't be split up).

I figured it out! SelectFirst is not a function in my version of Mathematica. But by changing the code to First[Select[... it works as expected. I stared at that for hours before it finally dawned on me that SelectFirst should not be blue after I evaluate the cell, unless it's not been given and assignment.

Any suggestions on what I can replace CirclePoints and Association with? They are also mathematica 10 commands. I guess I really do need to hassle the IT department for an upgrade.

And Association can be avoided by replacing the two consecutive lines as follows:

lines = Thread[numbers -> pos];
lines = Map[# /. lines &, sol, {2}];