Message Boards Message Boards

Best NDSolve Methods for this equation?

Fernando Garcia, UPM
Posted 8 years ago

Hello everybody!

First, thank you for reading this post.

I am a Ph.D. student in plasma physics, and I am struggling with numerically solving a set of equations. After some thoughts, I basically detected that the problem in my solution arises from my inability to choose good NDSolve methods to solve an inherently unstable equation of the type:

dy/dt = - d^2y/dx^2,

With initial condition y(x,0) = sin(x), and boundary conditions y(0,t) = 0, y(Pi,t) = 0.

The analytical solution is y(x,t) = Exp(t)Sin(x), but I failed to compute it numerically. An example: 

solpru = NDSolve[{D[y[x, t], t] == - D[D[y[x, t], x], x], 
    y[0, t] == Sin[0], y[Pi, t] == Sin[Pi], y[x, 0] == Sin[x]}, 
   y, {x, 0, Pi}, {t, 0, 1}, Method -> {
     "PDEDiscretization" -> {"MethodOfLines", 
       "SpatialDiscretization" -> {"TensorProductGrid"}}}];
ys[x_,t_] := Evaluate[y[x,t] /. solpru];
Plot[{ys[x, 0], ys[x, 1]}, {x, 0, Pi}, PlotRange -> All]

I have tried with different Mehtods ("TimeIntegration", "PDEDiscretization"), but none of them gave me a proper result, all of them induced numerical instabilities.

Please can someone shed some light on this problem? Which would the best Method options be for this type of "exploding" equation?

Thank you very much
POSTED BY: Fernando Garcia
4 Replies
Sort By:
Eric Meyers
Eric Meyers
Posted 8 years ago

This works pretty well. Numeric ....

solpru = NDSolve[{D[y[x, t], t] == -D[D[y[x, t], x], x], 
    y[0, t] == Sin[0], y[Pi, t] == Sin[Pi], y[x, 0] == Sin[x]}, 
   y, {x, 0, Pi}, {t, 0, 1}, MaxSteps -> Infinity, PrecisionGoal -> 3,
    AccuracyGoal -> 8, 
   Method -> {"MethodOfLines", 
     "SpatialDiscretization" -> "FiniteElement"}];

    Plot3D[Evaluate[y[x, t] /. solpru], {x, 0, Pi}, {t, 0, 1}]

enter image description here

Analytical

sol2 = DSolve[{D[y[x, t], t] == -D[y[x, t], {x, 2}], 
y[0, t] == Sin[0], y[Pi, t] == Sin[Pi], y[x, 0] == Sin[x]}, 
y, {x, 0, Pi}, {t, 0, 1}]

{{y -> Function[{x, t}, E^t Sin[x]]}}

analytical
POSTED BY: Eric Meyers

Thank you very much.

The discretization using Finite Elements work for this case. However, I have noticed that the FiniteElement discretization apparently does not work when the coefficients of the equation are not polynomials of the unknowns. For example:

dy/dt = -1/(1+y) d^2 y/dx^2.

Would you know how to overcome this problem?

Thank you!
POSTED BY: Fernando Garcia

Hey. First ,I don't know the best Method options for this type,but this code below works:

ppR = 20;
solpru = NDSolve[{D[y[x, t], t] == -D[D[y[x, t], x], x], 
    y[0, t] == Sin[0], y[Pi, t] == Sin[Pi], y[x, 0] == Sin[x]}, 
   y, {x, 0, Pi}, {t, 0, 1}, MaxSteps -> Infinity, PrecisionGoal -> 1,
    AccuracyGoal -> 1, 
   Method -> {"MethodOfLines", 
     "SpatialDiscretization" -> {"TensorProductGrid", 
       "MinPoints" -> ppR, "MaxPoints" -> ppR, 
       "DifferenceOrder" -> 1}, 
     Method -> {"ExplicitEuler", "MaxDifferenceOrder" -> 4}}];
ys[x_, t_] := Evaluate[y[x, t] /. solpru];
Plot[{ys[x, 0], ys[x, 1/2], ys[x, 3/4], ys[x, 1]}, {x, 0, Pi}, 
 PlotRange -> All]

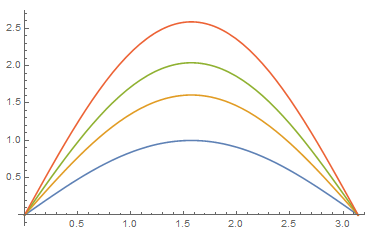
enter image description here

See another code:

ppR = 50;
solpru = NDSolve[{D[y[x, t], t] == -D[D[y[x, t], x], x], 
    y[0, t] == Sin[0], y[Pi, t] == Sin[Pi], y[x, 0] == Sin[x]}, 
   y, {x, 0, Pi}, {t, 0, 1}, MaxSteps -> Infinity, PrecisionGoal -> 1,
    AccuracyGoal -> 1, 
   Method -> {"MethodOfLines", 
     "SpatialDiscretization" -> {"TensorProductGrid", 
       "MinPoints" -> ppR, "MaxPoints" -> ppR, 
       "DifferenceOrder" -> 1}, 
     Method -> {"ImplicitRungeKutta", "DifferenceOrder" -> 2}}];
ys[x_, t_] := Evaluate[y[x, t] /. solpru];
Plot[{ys[x, 0], ys[x, 1/2], ys[x, 3/4], ys[x, 1]}, {x, 0, Pi}, 
 PlotRange -> All]
POSTED BY: Mariusz Iwaniuk

Thank you very much!

I see that the key point here is to lower the requirements on precision and accurary goals.

Comparing with the analytic solution, it turns out that the integration with the Implicit Runge Kutta is better than the Explicit Euler.

Best,

Fernando
POSTED BY: Fernando Garcia
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract