MMA can find symbolic solution to this function. :)
ClearAll["Global`*"];
Remove["Global`*"];
f[x_, y_] := Sqrt[x Exp[-x/a]] Sqrt[y Exp[-y/a]] (1 - Exp[c*I (x + y)])/((x + y) (y - b))
solving for x:
sol = Integrate[f[x, y], {x, 0, Infinity}, Assumptions -> {{a, b, c, y} > 0, {a, b, c, y} \[Element] Reals}, PrincipalValue -> True]
(*(1/(Sqrt[1 - 2 I a c] (-b + y)))Sqrt[
E^(-(y/a)) y] (Sqrt[a] Sqrt[1 - 2 I a c] Sqrt[2 \[Pi]] -
Sqrt[a] E^(I c y) Sqrt[2 \[Pi]] +
E^(y/(2 a)) \[Pi] Sqrt[y - 2 I a c y] -
E^(y/(2 a)) \[Pi] Sqrt[y - 2 I a c y]
Erf[(Sqrt[1/a - 2 I c] Sqrt[y])/Sqrt[2]] -
Sqrt[1 - 2 I a c] E^(y/(2 a)) \[Pi] Sqrt[y]
Erfc[Sqrt[y/a]/Sqrt[2]])*)
sol1 = FullSimplify[sol, Assumptions -> {a, b, y, c} > 0]
(*(1/(Sqrt[1 - 2 I a c] (-b + y)))Sqrt[
E^(-(y/a)) y] (Sqrt[a] (Sqrt[1 - 2 I a c] - E^(I c y)) Sqrt[
2 \[Pi]] +
E^(y/(2 a)) \[Pi] (Sqrt[y - 2 I a c y]
Erfc[(Sqrt[1/a - 2 I c] Sqrt[y])/Sqrt[2]] -
Sqrt[1 - 2 I a c] Sqrt[y] Erfc[Sqrt[y/a]/Sqrt[2]]))*)
solving for y:
sol2 = Integrate[sol1, {y, 0, Infinity}, Assumptions -> {{a, b, c} > 0, {a, b, c} \[Element] Reals}, PrincipalValue -> True]
(* 2 a \[Pi] -
2 Sqrt[2] Sqrt[a] Sqrt[b] \[Pi] DawsonF[Sqrt[b/a]/Sqrt[2]] + (
Sqrt[a] Sqrt[
2 \[Pi]] (-(Sqrt[2 \[Pi]]/Sqrt[1/a - 2 I c]) +
Sqrt[b] E^(-(b/(2 a)) + I b c) \[Pi] Erfi[(
Sqrt[b] Sqrt[1/a - 2 I c])/Sqrt[2]]))/Sqrt[
1 - 2 I a c] - (\[Pi] (b^2 HypergeometricPFQ[{1, 1}, {3/2, 2}, -(b/(
2 a))] +
a (a - b EulerGamma - b Log[2] + b Log[a] - b Log[b])))/a + (1/(
a (1 - 2 I a c)))\[Pi] (-b^2 (I + 2 a c)^2 HypergeometricPFQ[{1,
1}, {3/2, 2}, -(b/(2 a)) + I b c] +
a (a - b EulerGamma + 2 I a b c EulerGamma - b Log[2] +
2 I a b c Log[2] + (b - 2 I a b c) Log[a] +
b (-1 + 2 I a c) Log[b] - b Log[1 - 2 I a c] +
2 I a b c Log[1 - 2 I a c]))*)
sol3 = FullSimplify[sol2, Assumptions -> {{a, b, c} > 0, {a, b, c} \[Element] Reals}]
(*\[Pi] ((2 a (I + a c - (I Sqrt[a] Sqrt[1/a - 2 I c])/Sqrt[
1 - 2 I a c]))/(I + 2 a c) -
2 Sqrt[2] a Sqrt[b/a] DawsonF[Sqrt[b]/(Sqrt[2] Sqrt[a])] + (
2 Sqrt[2] Sqrt[a] Sqrt[b]
DawsonF[(Sqrt[b] Sqrt[1/a - 2 I c])/Sqrt[2]])/Sqrt[
1 - 2 I a c] - (
b^2 HypergeometricPFQ[{1, 1}, {3/2, 2}, -(b/(2 a))])/a + (
b^2 (1 - 2 I a c) HypergeometricPFQ[{1, 1}, {3/2, 2}, -(b/(2 a)) +
I b c])/a - b Log[1 - 2 I a c])*)
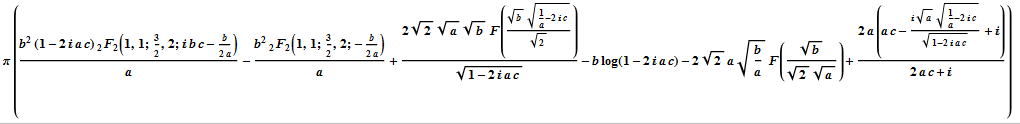
sol3 /. a -> 100 /. b -> 1/1000 /. c -> 1000 // N
(* 314.121 + 0.00134748 I *)