Please see video of chaotic map animation here:
While showing a few thousand points gives one a feeling about a chaotic map
iterations = Compile[{orbit, angle, {n, _Integer}},
Module[{x, y, l, k, cs = Cos[angle], sn = Sin[angle], \[Sigma]},
x = orbit;
y = orbit;
l = Table[{0., 0.}, {n}];
k = 0;
While[k < n && Abs[x] + Abs[y] < 10^3,
\[Sigma] = x^2 - y;
{x, y} = {x cs + \[Sigma] sn, x sn - \[Sigma] cs};
k++; l[[k]] = {x, y}];
Take[l, k]
], CompilationOptions -> {"ExpressionOptimization" -> True}
]
Manipulate[
Graphics[{PointSize[0.002],
Point[Flatten[
Table[iterations[x, \[Alpha], Round[10^n]], {x, 0, xm, xm/p}],
1]]}, PlotRange -> 2],
{{\[Alpha], 1.3, "angle"}, 0, 2 Pi},
{{xm, 1.5, "max x"}, 0.1, 3},
{{p, 50, "steps"}, 2, 100, 1},
{{n, 2.5, "iterations"}, 1, 4}]
often one needs million points to see many of the details.
So, instead of showing points directly, we accumulate and bin the points using:
toMatrixEntries[l_, dim_] :=
Module[{L = 1.25}, SparseArray[ Rule @@@ Select[Tally[
Ceiling[dim Transpose[Transpose[l] + L {1, 1}]/(2 L)]],
(1 <=
Min[#] && Max[#] <= dim) &], {dim, dim}]]
makeReliefPlot[mat_] :=
With[{logmax = Log@Max[mat]},
ReliefPlot[mat, PlotRange -> All, Frame -> False,
ColorFunctionScaling -> False,
ColorFunction -> (If[# == 0, Gray,
ColorData["DarkRainbow"][1. Log[#]/logmax]] &),
ImageSize -> 600]]
For instance
mat = 0;
Monitor[Do[
mat = mat + toMatrixEntries[iterations[orbit, 1.34, 10000], 1200],
{orbit, -1.25, 1.25, 0.001}];,
Row[{"orbit: ", orbit}]] ;
rp = makeReliefPlot[mat];
makeReliefPlot[mat]
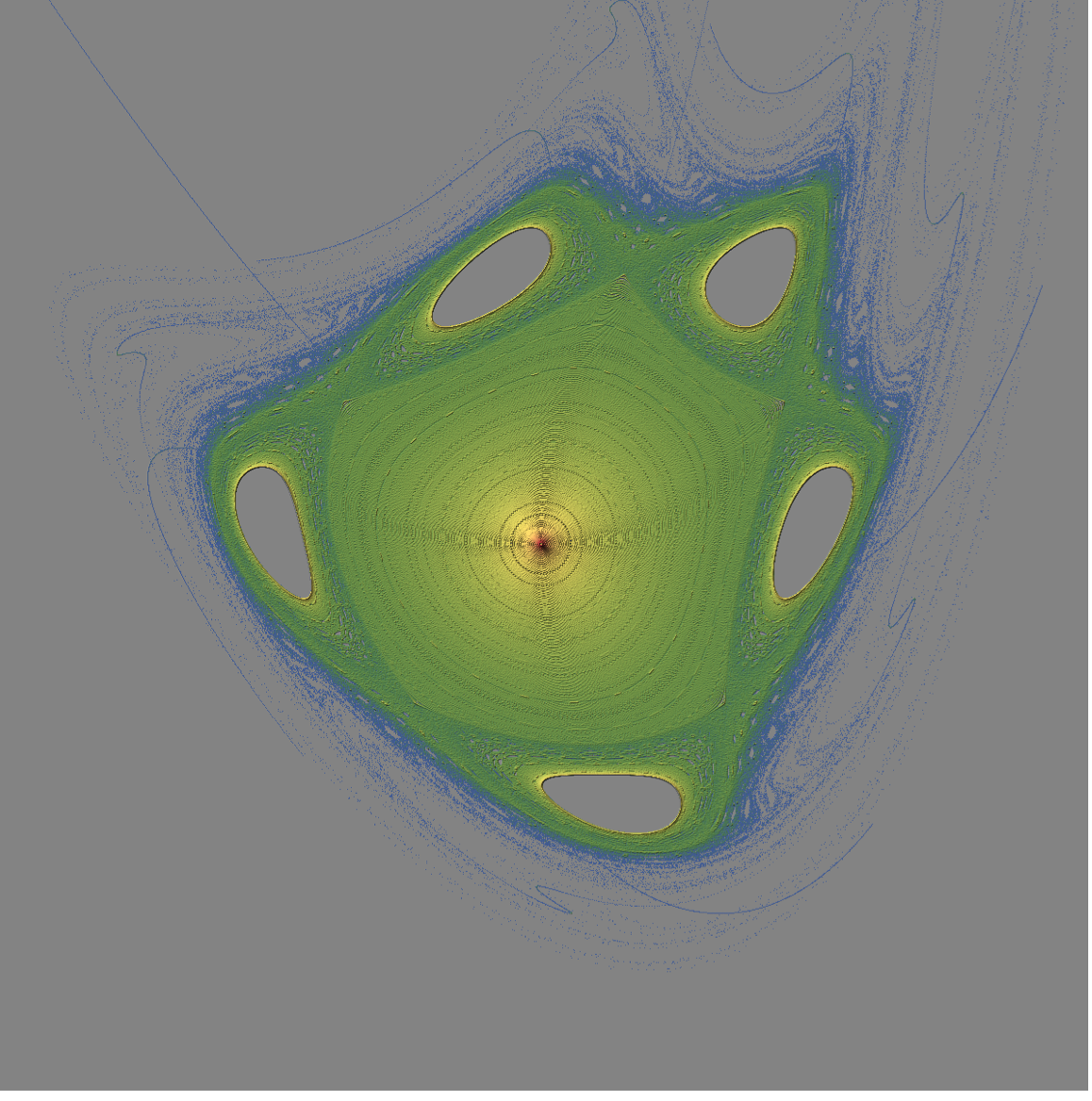
Now doing this for varying angle, we can get the above animation.