The long evolutionary history of humans has optimized the recognition of animals in the human vision system. To escape predators and to find food. Sometimes we believe to see animals and human faces, even if there aren't any, this phenomena is called pareidolia, or more generally apophenia. Classic examples are Jesus on a toast (Liu2014), the image on the shroud of Turin (Sheen2016), Elvis in a potato chip (Voss2011), and the face on Mars (Martinez-Conde2012). In many cases, in about 100ms (Naber2012) humans can identify animal shapes. Some animals, e.g. snakes are potentially identified much faster (VanLe2013).
So, an interesting question might be: how often do we (believe to) see animals in an genuinely random image?
Here is, in the literal sense of the word, a random image of size 300*300 pixels:
SeedRandom[4056380];
dim=300;
randomImage = Image[Table[RandomChoice[{2,1}->{0,1}],{dim},{dim}]];
Show[randomImage,ImageSize -> 300]

No animal shapes are directly visible.
Using ImageMesh we can get the individual/connected components (some potentially animal-like shaped) as regions (this operation is not fully deterministic, so results below may vary).
Show[imesh=ImageMesh[randomImage,Method->"DualMarchingSquares"],ImageSize -> 300]

These are the individual shapes. We ignore too small and too large regions. For our image we find neatly 400 regions.
(* this takes a minute *)
shapes=Select[ConnectedMeshComponents@imesh,18< Area[#]<2000&];
Length[shapes]
393
These are the shapes positioned in the original image.
Show[HighlightMesh[#,Style[2, RandomColor[]]]&/@ shapes]

For later use, we define one function to make a random image and get the shapes.
getShapes[{black_,white_}, dim_] :=Select[ConnectedMeshComponents@
ImageMesh[Image[Table[RandomChoice[{black,white}->{0,1}],{dim},{dim}]],
Method->"DualMarchingSquares"],18< Area[#]<2000&]
As we want to interpret the shapes as animals, we smooth the edges. We switch from regions to graphics.
smooth[reg_] :=Graphics[{Lighter[Blue],
(ToExpression[ToString[InputForm@reg],StandardForm,Hold] /.
HoldPattern[BoundaryMeshRegion[v_,b__,___Rule]]:>GraphicsComplex[v,FilledCurve[{b}/.
Line[l_]:> BSplineCurve[DeleteDuplicates[Flatten[l,1]],
SplineClosed->True,SplineDegree->2]]])[[1]]}]
We also allow changing the orientation and color.
rotate[g_,?_] := With[{m={{Cos[?],Sin[?]},{-Sin[?], Cos[?]}}},g/.
GraphicsComplex[v_, r__]:> GraphicsComplex[m.#&/@ v,r]]
flip[g_] := g/.GraphicsComplex[v_, r__]:> GraphicsComplex[{-1,1}#&/@ v,r]
recolor[g_,col_] := g/.c_RGBColor:>col
animalize[g_,{f_,?_,col_}] := Graphics[ recolor[rotate[If[f, flip,Identity]@
smooth[g],?],col], PlotRange -> All]&[smooth[g]]
Here are some of the shapes that were hiding in the above image.The human eye tries to see fishes, wales, birds, squirrels, frogs, ducks, sea-horses, bunnies, deers, dogs, cats and similar creatures as well as human heads.
GraphicsGrid[Partition[Show[#, ImageSize -> 120,Frame->True,FrameTicks->False]&/@#,5]&@
{ animalize[shapes[[18]],{False,1.8,GrayLevel[0.1]}],
animalize[shapes[[99]],{False,1.1,Darker[Yellow]}],
animalize[shapes[[6]],{False,0.7,Darker[Blue]}],
animalize[shapes[[14]],{False,0.,Darker[Brown]}],
animalize[shapes[[4]],{False,0.5,Darker[Red]}],
animalize[shapes[[23]],{False,0,Darker[Orange]}],
animalize[shapes[[76]],{False,0,Darker[Orange,0.6]}],
animalize[shapes[[95]],{False,-1.5,Darker[Green,0.4]}],
animalize[shapes[[9]],{False,0.,Brown}],
animalize[shapes[[163]],{False,1.1,Darker[Purple]}]},
Spacings->{5,-20}]

Looking at the last selection shows the importance of one or two eyes in the shapes (Yang2015). Eyes are often used by nature for deception (Steven2014).
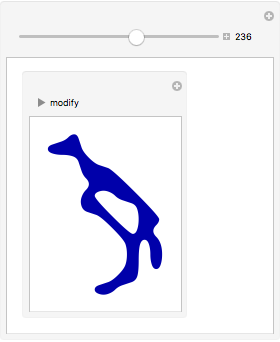
A small Manipulate will allow to optimize the animal-perception by changing color, orientation, and aspect ratio.
makeManipulate[shape_]:=Manipulate[Graphics[ recolor[rotate[If[f, flip,Identity]@ #[[1]],?],col],
ImageSize -> 120,AspectRatio->ar,PlotRange -> All],
OpenerView[{"modify",Column[{
Control[{{?,0,"rotate"},-Pi,Pi,ImageSize->Small}],
Control[{{f,False,"reflect"},{True,False},ImageSize->Small}],
Control[{{col, Darker[Blue],"color"},Red,ImageSize->Tiny}],
Control[{{ar, Automatic,"aspect ratio"},0.2,5,ImageSize->Small}]}]}],
SaveDefinitions->True,TrackedSymbols:>True]&[smooth[#]]&@ shape
Manipulate[makeManipulate[shapes[[j]]],{{j,141,""},1, Length[shapes],1,Appearance->"Labeled"}]
Here are some more animal-shapes found in other random images.

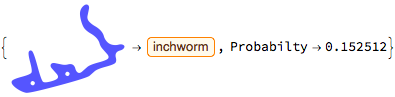
One could now try to automate the finding of animals using ImageIdentify. In general, the interpretation of ImageIdentify will depend on the image orientation. So, we maximize over different orientations.
getOptimalAnimal[shape_] :=
Module[{s=smooth[shape][[1]],tab,ras,tab2},
tab=Table[{(ras=Rasterize[Graphics[rotate[s,\[Alpha]],ImageSize -> 120,PlotRange -> All]]),
Normal@KeyDrop[ImageIdentify[ras,"animal",2,"Probability"],Entity["Concept",#]&/@
{"Person::93r37","Hominid::tt93h","Mammal::nt5bz",
"SeaStar::46w97","Shark::632s8","CanisFamiliaris::597qc"}]},
{\[Alpha], 0, 2Pi, 2Pi/24}];
tab2=Sort[{#2[[1,2]], #2[[1,1]], #1}&@@@DeleteCases[ tab,{_,{}}]];
{tab2[[-1,3]]->tab2[[-1,2]],"Probabilty" -> tab2[[-1,1]]}]
As ImageIdentify was trained on real photographs, it is not the ideal tool for this task. It is biased towards humans, mammals, and sharks.
getOptimalAnimal[shapes[[10]]]

getOptimalAnimal[shapes[[27]]]
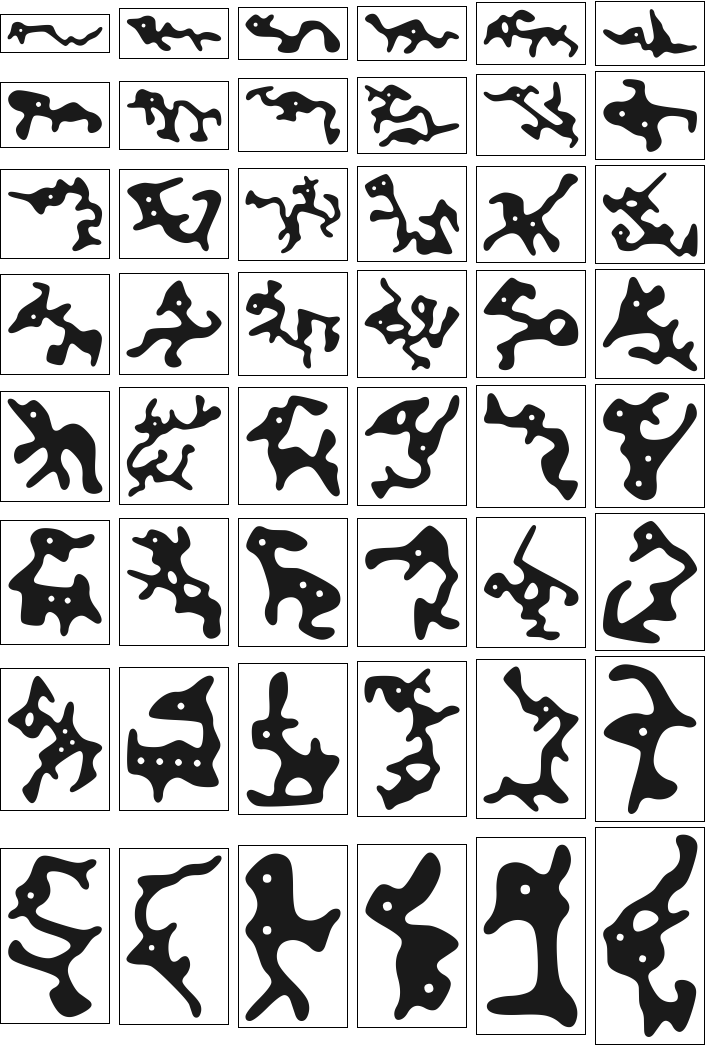
To answer the original question: in a random 400x400 pixel image, one easily finds a few dozen animals. Here are four dozen animal-shape like smoothed regions from random 400x400 image.
Module[{gs, gs2},
SeedRandom[2222];
gs = getShapes[{2, 1}, 400];
gs2 = {animalize[gs[[3]], {False, 0, GrayLevel[0.1]}],
animalize[gs[[6]], {False, 1, GrayLevel[0.1]}],
animalize[gs[[9]], {False, 1.3, GrayLevel[0.1]}],
animalize[gs[[15]], {False, -1, GrayLevel[0.1]}],
animalize[gs[[17]], {False, 0.3, GrayLevel[0.1]}],
animalize[gs[[30]], {True, 2.3, GrayLevel[0.1]}],
animalize[gs[[39]], {False, 0.3, GrayLevel[0.1]}],
animalize[gs[[40]], {True, -0.1, GrayLevel[0.1]}],
animalize[gs[[48]], {False, -0.1, GrayLevel[0.1]}],
animalize[gs[[53]], {True, -0.1, GrayLevel[0.1]}],
animalize[gs[[55]], {True, -0.1, GrayLevel[0.1]}],
animalize[gs[[62]], {True, 2.3, GrayLevel[0.1]}],
animalize[gs[[64]], {False, 0, GrayLevel[0.1]}],
animalize[gs[[65]], {False, 0, GrayLevel[0.1]}],
animalize[gs[[68]], {False, -0.2, GrayLevel[0.1]}],
animalize[gs[[73]], {True, -0.3, GrayLevel[0.1]}],
animalize[gs[[81]], {False, 0.2, GrayLevel[0.1]}],
animalize[gs[[86]], {True, 3.4, GrayLevel[0.1]}],
animalize[gs[[97]], {False, 0.3, GrayLevel[0.1]}],
animalize[gs[[100]], {False, 0.9, GrayLevel[0.1]}],
animalize[gs[[101]], {False, 2.6, GrayLevel[0.1]}],
animalize[gs[[115]], {False, 4.3, GrayLevel[0.1]}],
animalize[gs[[124]], {False, 0, GrayLevel[0.1]}],
animalize[gs[[125]], {False, 2.9, GrayLevel[0.1]}],
animalize[gs[[139]], {False, 0, GrayLevel[0.1]}],
animalize[gs[[146]], {False, -1.6, GrayLevel[0.1]}],
animalize[gs[[175]], {False, -1., GrayLevel[0.1]}],
animalize[gs[[201]], {True, -0.5, GrayLevel[0.1]}],
animalize[gs[[209]], {True, 3.1, GrayLevel[0.1]}],
animalize[gs[[210]], {False, -1.4, GrayLevel[0.1]}],
animalize[gs[[218]], {True, 3.2, GrayLevel[0.1]}],
animalize[gs[[227]], {True, -0.3, GrayLevel[0.1]}],
animalize[gs[[229]], {True, 0.9, GrayLevel[0.1]}],
animalize[gs[[253]], {True, 0., GrayLevel[0.1]}],
animalize[gs[[273]], {True, -0.3, GrayLevel[0.1]}],
animalize[gs[[278]], {True, 1., GrayLevel[0.1]}],
animalize[gs[[282]], {True, 3, GrayLevel[0.1]}],
animalize[gs[[298]], {False, 0, GrayLevel[0.1]}],
animalize[gs[[299]], {False, 0.6, GrayLevel[0.1]}],
animalize[gs[[318]], {False, 2., GrayLevel[0.1]}],
animalize[gs[[326]], {False, 3, GrayLevel[0.1]}],
animalize[gs[[340]], {False, -1.3, GrayLevel[0.1]}],
animalize[gs[[352]], {True, -13, GrayLevel[0.1]}],
animalize[gs[[361]], {True, -13, GrayLevel[0.1]}],
animalize[gs[[365]], {False, 2.4, GrayLevel[0.1]}],
animalize[gs[[377]], {True, 2.6, GrayLevel[0.1]}],
animalize[gs[[395]], {False, 0.3, GrayLevel[0.1]}],
animalize[gs[[405]], {True, 0.3, GrayLevel[0.1]}]};
Grid[Partition[Framed[Show[#, ImageSize -> 100]] & /@
SortBy[gs2, FullOptions[#, AspectRatio] &], 6]]]

Using different method options for ImageMesh gives different results. Here are some animal-shaped regions from a 300*300 image and method "MarchingSquares".
