Please use the following code form the demonstration Pursuit Curves by @Michael Trott:
pursuitGraphics[{x0_,y0_},T_,v_,?_]:=
Module[{},
X[t_]=(1-? t) Cos[t];
Y[t_]=(1-? t) Sin[t];
nds=NDSolve[{Thread[{
x'[t],y'[t]}==v {X[t]-x[t],
Y[t]-y[t]}/Sqrt[(X[t]-x[t])^2+(Y[t]-y[t])^2]],
x[0]==x0,y[0]==y0},{x,y},{t,0,T},
PrecisionGoal->4,
StoppingTest:>((X[t]-x[t])^2+(Y[t]-y[t])^2<10^-3)];
tm=nds[[1,1,2,1,1,2]];
Show[{
ParametricPlot[Evaluate[{X[t],Y[t]}],{t,0,tm},
PlotStyle->{{Thickness[0.002],Black}}, PlotRange -> All,MaxRecursion->ControlActive[2,6]],
ParametricPlot[Evaluate[{x[t],y[t]}/.nds[[1]]],{t,0,tm},
PlotStyle->{Thickness[0.005]},
ColorFunction->(Blend[{RGBColor[.8,1,0],RGBColor[1,.8,0],RGBColor[0,.75,0.02],RGBColor[0,.5,1]},#3]&),
PlotRange->All,MaxRecursion->ControlActive[2,6]]}, PlotRange -> 2,
Frame->False,Axes->False,FrameTicks->None,ImageSize->{400,400}]]
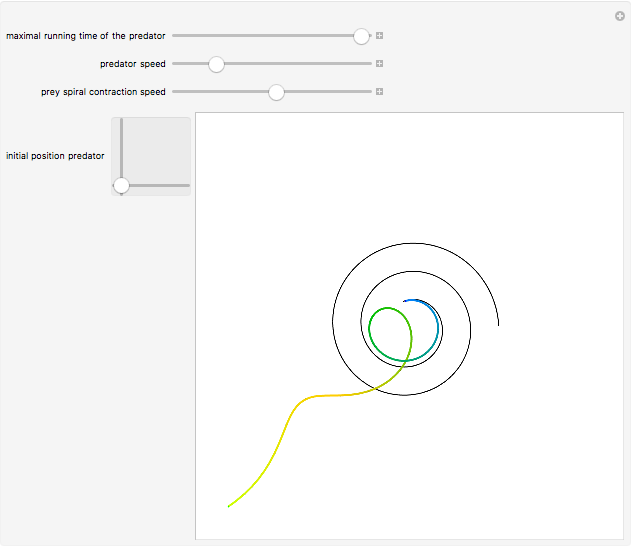
Manipulate[
pursuitGraphics[xy0, T,v, ?] ,
{{T,40,"maximal running time of the predator"},1, 100},
{{v, 0.894,"predator speed"},0, 2},
{{?,0.01,"prey spiral contraction speed"},-1, 1},
{{xy0,{-1.03, -0.21},"initial position predator"},{-2,-2},{2,2}},
ControlPlacement->{Top,Top,Top,Left},SaveDefinitions->True]