Hi All, I have sets of FFT's. plotted 2D. I want to draw all ofthem in 3D with sampling . Other question how can I draw maximum peak points of this plot? FFTdbD is my function, I partitioned data to 36 sample. I just get FFT of each sample. I need to compare peaks or draw all FFTs in 3D.

Table[ListLinePlot[FFTdBD[data3[[All, x]], fs], Joined -> True, PlotRange -> {{0, 25}, All}, GridLines -> Automatic, Frame -> True, FrameLabel -> {"Frequency (Hz)", "a(t)(dB)"}, LabelStyle -> Directive[Black, Thin], PlotStyle -> Red], {x, 1, 36, 1}]

Thanks for your help.

General! Example: [Sin[x]^n] where: 0<x<3 and 1<n<5 Can we plot and show 5 -separated- "3D" graphs of sinx all in one 3D graph?

Is it possible to plot 3D graphs into 3D system of coordinates?? In other words, in these algorithms we plotted 2D graphs in 3D system, how to plot their 3D forms all in one 3D system of coordinates?? I would be really appreciate if you help me.

Great! Thanks a lot

Thank You Very Much! My last question is about the filling part. In mathematica we can use fillingstyle to change the color of filling part. In this algorithm the filling part is blue. I would be really appreciate if you help me to change the color either.

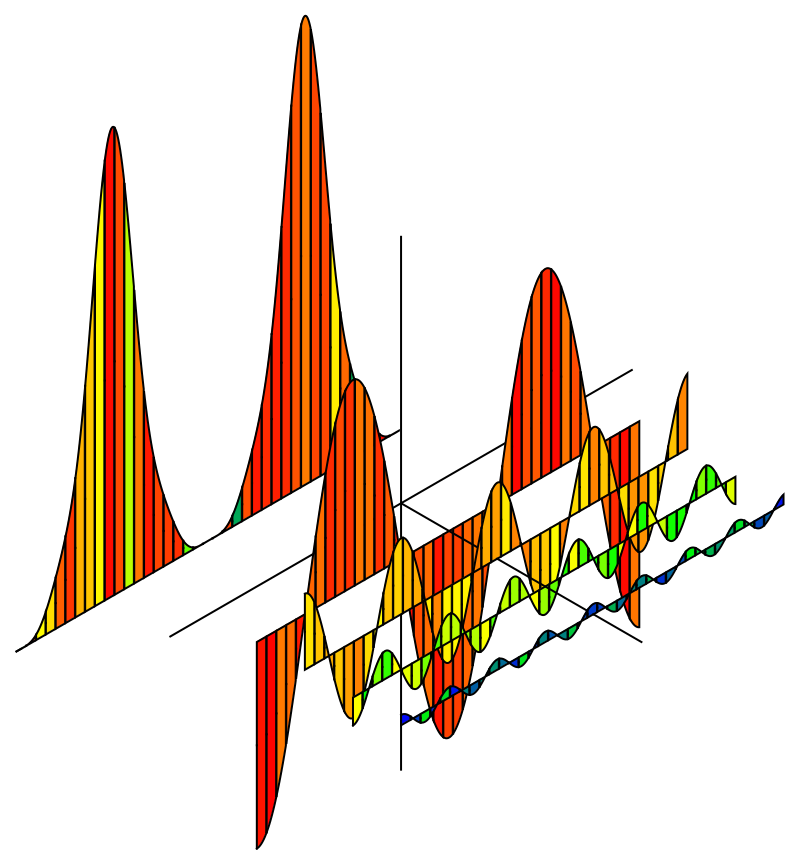
Hi Jesus,

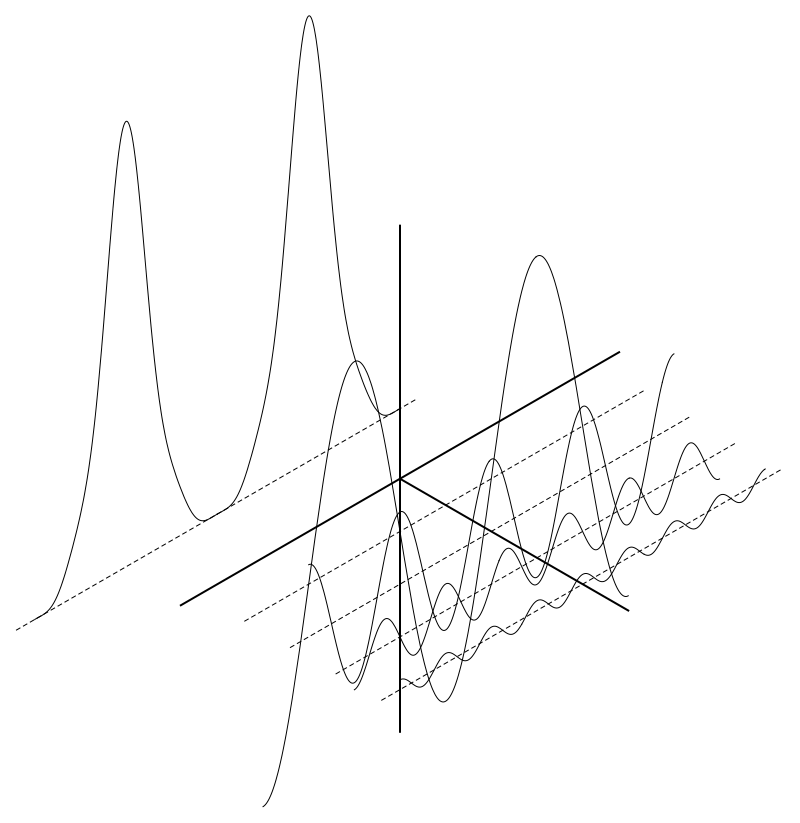
Your picture is an isometric line drawing. All such images are easy to draw by constructing the three dimensional curves, choosing the view vectors, and projecting into the plane. If you get more detailed, the main difficulty becomes the ordering and stacking along the axis of projection. I think it's advantageous to use Graphics as opposed to Graphics3D because the output of Graphics is a scalable vector, seems to be more reliable for including in papers. I've already given a few examples in a recent topic:

Plotting the Contours of Deformed Hyperspheres

Here's another example more along the lines of what you are looking for:

Function Definitions

Amp = Normalize[(-1)^# Exp[-#] & /@ Range[4]];
fs = Times[Cos[k x] /. k -> (# 2 Pi) & /@ Range[4], Amp];
F = Total[fs];
f0 = -(F /. x -> 0);
F2 = f0 + F;

View Settings

ViewV = Normalize@ {1, -1, 1};
xOrtho = Normalize@{1, 1, 0};
yOrtho = Normalize@Cross[ViewV, xOrtho];
Projector = {xOrtho, yOrtho};
colors = Partition[{Red, Orange, Yellow, Green, Blue}, 2, 1];
intRatio = {25, 9, 3, 2};

Curve to Points

GetLine[fx_, xm_, xp_] :=  Cases[Plot[fx, {x, xm, xp}, PlotRange -> All], Line[_], Infinity]
GetLine[fx_, xm_, xp_, n_, m_] :=  Join[#, {{#[[-1, 1]], 0}, {#[[1, 1]], 0}} ] & /@ Partition[
With[{nMax = Max[Flatten[Partition[Range[0, n], m, m - 1]]]},
N[Map[{(xm + # (xp - xm)), fx /. x -> (xm + # (xp - xm))} &, 
Range[0, nMax - 1]/(nMax - 1)]]  ], m - 1, m]    

Simple Output

Graphics[Join[
MapThread[{{Dashed, 
Line[Projector.# & /@ {{#2/4, -1.1, 0}, {#2/4, 1.1, 0}}]},
GetLine[#1, -1, 1] /. {y_, z_} :> Projector.{#2/4, y, z}} &,
{fs, Range[4]}],
{{Thick, Line[Projector.# & /@ {{0, 0, 0}, {5/4, 0, 0}}], 
Line[Projector.# & /@ {{0, 0, -1.2}, {0, 0, 1.2}}],
Line[Projector.# & /@ {{0, -1.2, 0}, {0, 1.2, 0}}]}, {
{Dashed, Line[Projector.# & /@ {{-1, -1.1, -f0}, {-1, 1.1, -f0}}]},
GetLine[F, -1, 1] /. {y_, z_} :> Projector.{-1, y, z}
}}], ImageSize -> 800]

Color Line Drawing

g1 = Graphics[{EdgeForm[Thick], MapThread[{#1, #2} &,
{RandomSample[
Flatten[MapThread[
Table[Blend[#1, RandomReal[{0, 1}]], {#2}] &, {colors, 
intRatio}]]],
Polygon[# /. {y_, z_} :> Projector.{-1, y, z - f0}] & /@ 
GetLine[F2, -1, 1, 2000, 50]}]}];

Show[ g1, Graphics[{Thick,
Line[Projector.# & /@ {{0, 0, 0}, {1/4, 0, 0}}],
Line[Projector.# & /@ {{0, -1.2, 0}, {0, 1.2, 0}}],
Line[Projector.# & /@ {{0, 0, -1.2}, {0, 0, 1.2}}]}],
MapThread[DrawPart, {fs, Range[4]/4, Table[1/4, {4}], colors}],  
ImageSize -> 800]

How about this:

Graphics3D[
 Table[Plot[Sin[n x], {x, 0, 2 Pi}, Filling -> Axis][[1]] /. 
   GraphicsComplex[pts_, other__] :> 
    GraphicsComplex[pts /. {x_Real, y_} :> {x, n, y}, other],
  {n, -3, 3, 1}]]

It makes 2D sin plots with Filling, and then lifts them into 3D.

Gianluca

I think was a very good One-Liner! Thanks again.

Jesus