At Wolfram Demonstrations, I perused the greater triangle center material that we had, including a new one.
Fate of the Euler Line and the Nine-Point Circle on the Sphere by Paolo Maraner
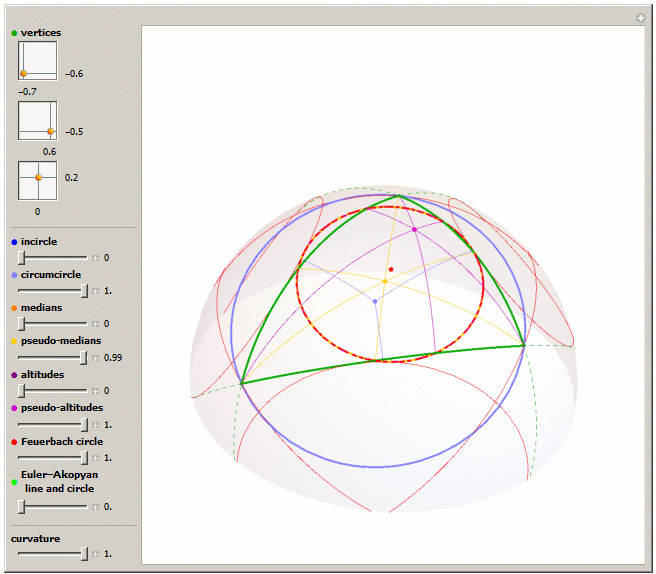
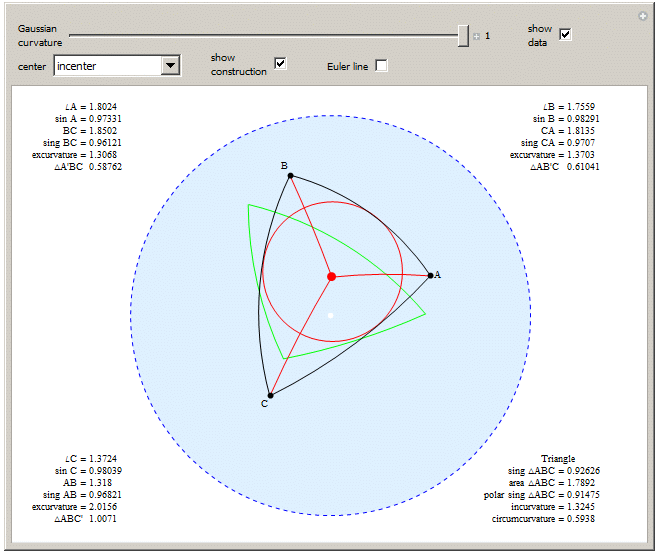
Non-Euclidean Triangle Continuum by Robert A. Russell
Tetrahedron Centers by Ed Pegg Jr
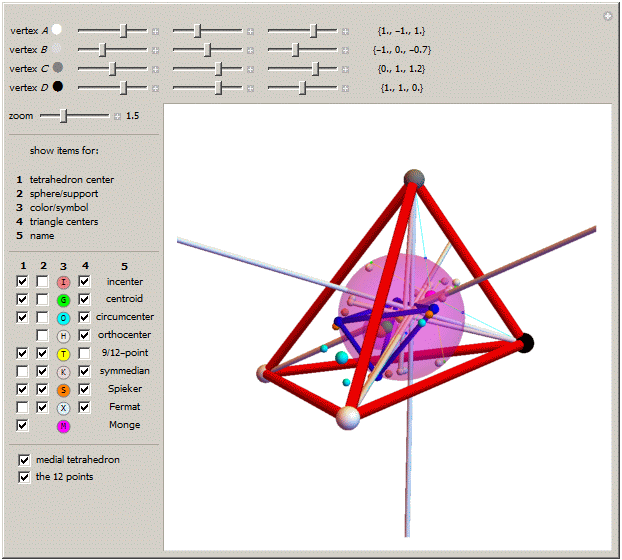
Also items like Triangle Calculator and Spherical Triangle Solutions, along with many recent submissions by Izidor Hafner. After writing the third demo above, I was surprised to rediscover the second, and astounded by the discussions in the first. In 2D euclidean space, these points in a triangle are known as Kimberling Centers. In 3D euclidean space, spherical geometry and hyperbolic geometry; many of these same points exist, but exact areal coordinates for them are not yet known. It seems like they should be findable, though, with this much interplay.