A couple of weeks ago I posted my first The Chaos Game post. This will be a continuation on that, exploring some new ideas. Please make sure to read the previous one first. And once you're finished with this post, read the continuation part III.
Colors
The first thing I wanted to try after my previous post was coloring. Let's color each of the points based on the point it jumps towards to:
ClearAll[sequence]
sequence[n_,m_]:=RandomChoice[Range[n],m]
Table[
circlepoints=N@CirclePoints[n];
seq=sequence[n,50000];
pts=Rest[FoldList[(#1+circlepoints[[#2]])/2&,RandomChoice[circlepoints],seq]];
plotdata=Transpose[{pts,seq}];
plotdata=SortBy[GatherBy[plotdata,Last],#[[1,2]]&];
plotdata=plotdata[[All,All,1]];
colors=ColorData[97]/@Range[n];
Rasterize[Graphics[{PointSize[0.001],Riffle[colors,Point/@plotdata],FaceForm[],EdgeForm[Black],RegularPolygon[n],PointSize[0.01],Riffle[colors,Point/@circlepoints]},ImageSize->{400,400},PlotRange->1.1],"Image",ImageSize->{400,400},RasterSize->{400,400}]
,
{n,3,8}
] // Partition[#,3]& // ImageAssemble
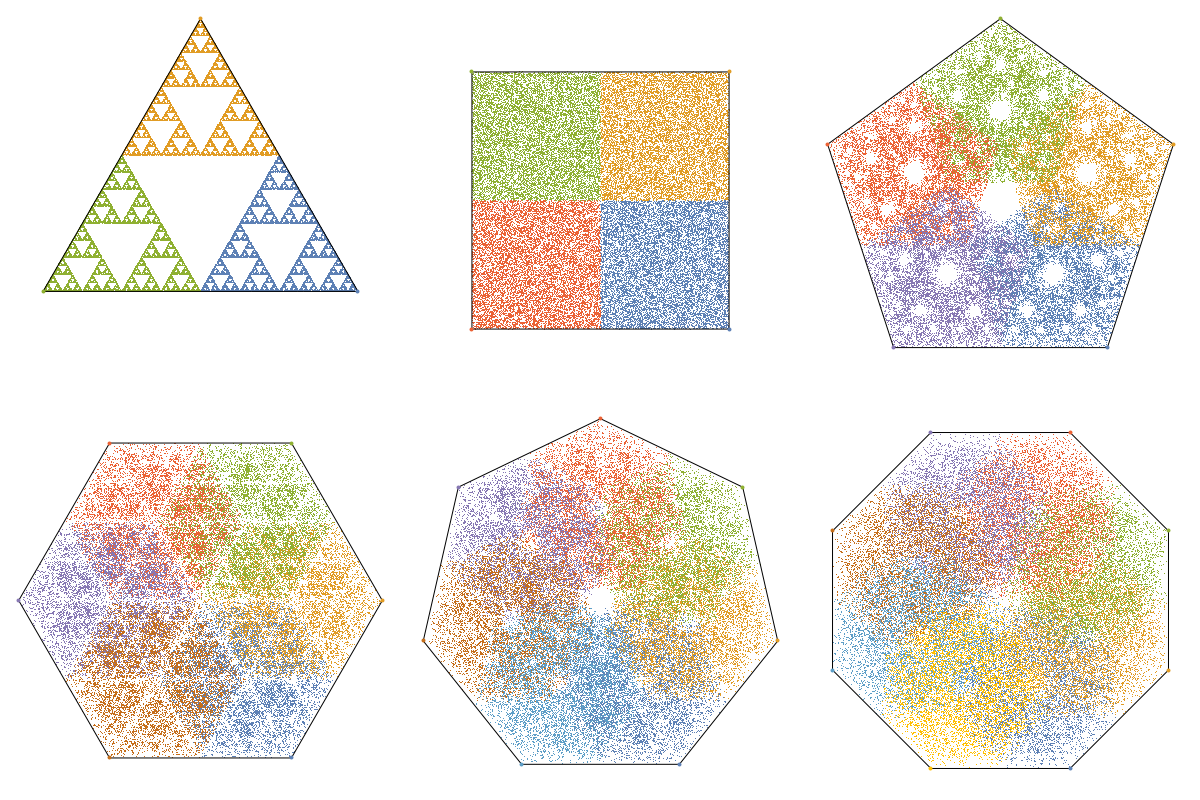
This explains why the regular triangle and the square have such an unique behavior; it does not 'blend'. To be more precise: the triangle only excludes spaces, and the square exactly covers the plane again. For higher order regular polygons you see that there is overlap and that creates high and low density regions creating a bunch of patterns.
For the case of restricted jumping, like we did last time, we can also do the coloring, here the modified code:
ClearAll[CreateSequence,CreateSequenceImage]
CreateSequence[n_,steps_,choices_]:=Mod[Accumulate[RandomChoice[choices,steps-1]~Prepend~1],n,1]
CreateSequenceImage[n_,m_,choices_]:=Module[{seq,circlepoints,pts,plotdata,colors},
seq=CreateSequence[n,m,choices];
circlepoints=N@CirclePoints[n];
pts=Rest@FoldList[(#1+circlepoints[[#2]])/2&,First[circlepoints],seq];
plotdata=Transpose[{pts,seq}];
plotdata=SortBy[GatherBy[plotdata,Last],#[[1,2]]&];
plotdata=plotdata[[All,All,1]];
colors=ColorData[97]/@Range[n];
Rasterize[Graphics[{FaceForm[],EdgeForm[Black],RegularPolygon[n],PointSize[0.001],Riffle[colors,Point/@plotdata],PointSize[0.03],Riffle[colors,Point/@circlepoints]},ImageSize->300,PlotRange->1.1],"Image",RasterSize->{300,300}]
]
Let's have a look at all the possible jumping-subsets for hexagons:
Grid[Join @@@
Partition[{#, CreateSequenceImage[6, 10^4, #]} & /@
Subsets[Range[6], {1, \[Infinity]}], UpTo[4]], Frame -> All]

Some really nice patterns are now created!
Fractional jumping
Up to now we have always jumped half-way, let's change that, and see what happens. I will introduce alpha the factor that we jump. Historically we always have set that to 0.5 (half-way). In my definition 0 means not moving, and 1 going all the way to the next point. The code can be easily modified:
ClearAll[sequence]
sequence[n_,m_]:=RandomChoice[Range[n],m]
FactorJump[n_,m_,\[Alpha]_]:=Module[{circlepoints,seq,pts,counts,img,bg},
circlepoints=N@CirclePoints[n];
seq=sequence[n,m];
pts=FoldList[(1-\[Alpha])#1+\[Alpha] circlepoints[[#2]]&,First[circlepoints],seq];
counts=Transpose@BinCounts[pts,{-1.1,1.1,0.005},{-1.1,1.1,0.005}];
counts=Reverse[counts];
img=Image[1-counts/Max[counts]];
bg=Graphics[Graphics[{FaceForm[],EdgeForm[Black],RegularPolygon[n],Text[NumberForm[\[Alpha],{\[Infinity],2}],{0,1.05}]},ImageSize->500,PlotRange->1.1]];
bg=Rasterize[bg,"Image",RasterSize->ImageDimensions[img],ImageSize->ImageDimensions[img]];
ImageMultiply[img,bg]
]
Note that I also included the plotting of the density of the points using BinCounts, which gives smooth images. Let's try it out with some new alpha:
FactorJump[3, 10^7, 0.3]
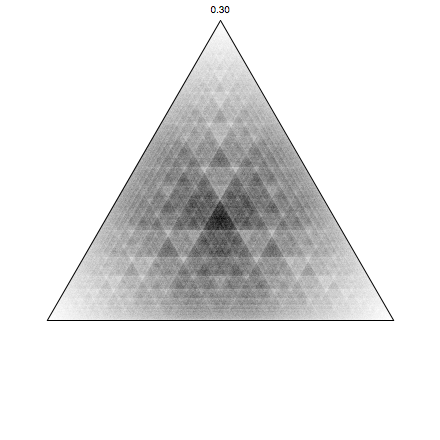
pretty nifty! Let's make a movie changing alpha gradually from 0 to 1:
n = 3;
imgs = Table[FactorJump[n, 3 10^5, \[Alpha]], {\[Alpha], 0, 1, 0.01}];
Export[ToString[n] <> "factor.gif", imgs, "DisplayDurations" -> 1/25.0]
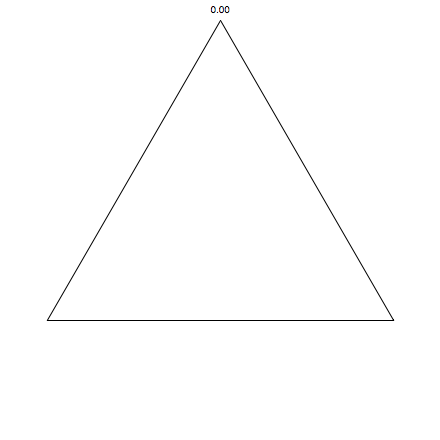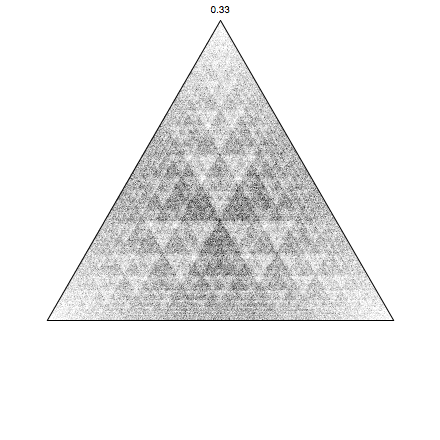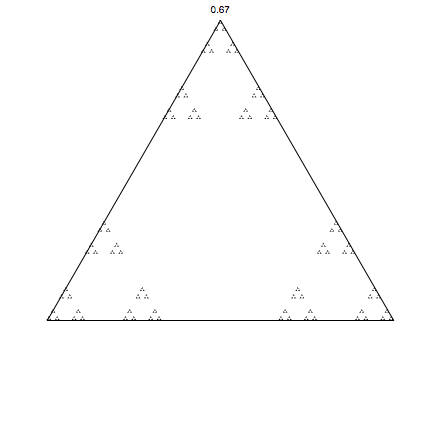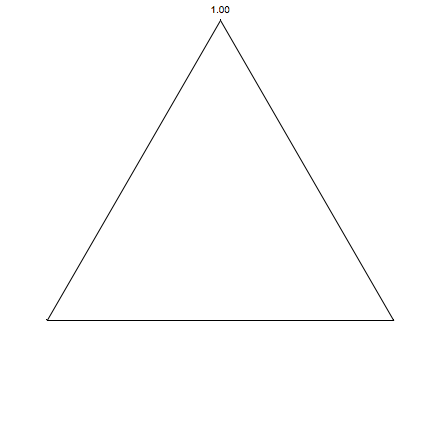
Now for squares:

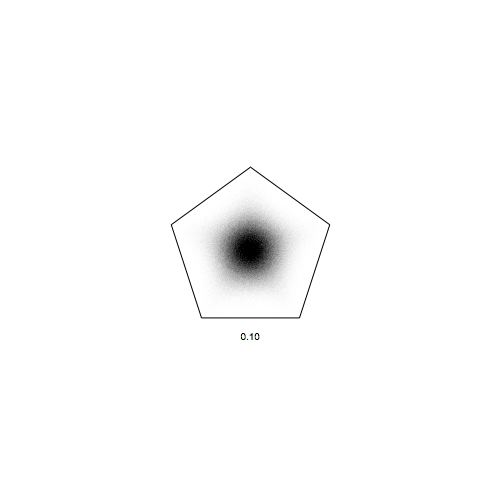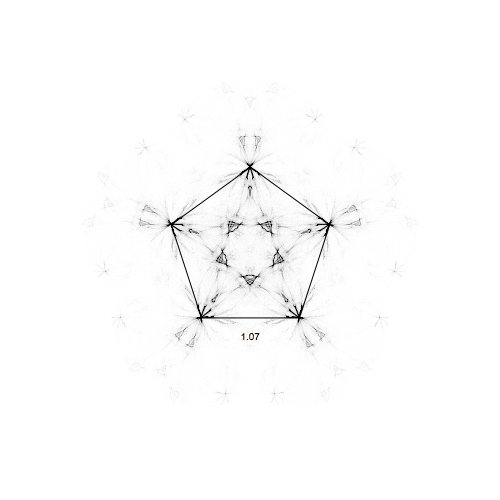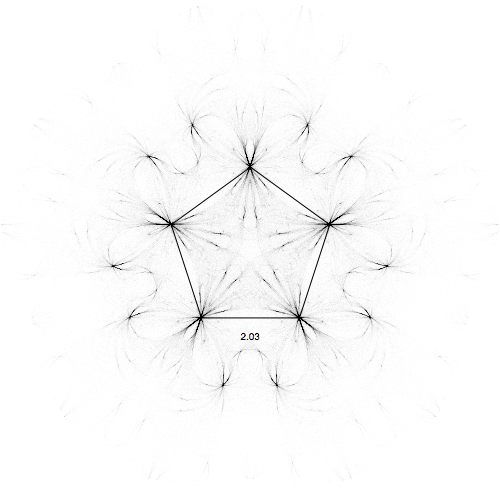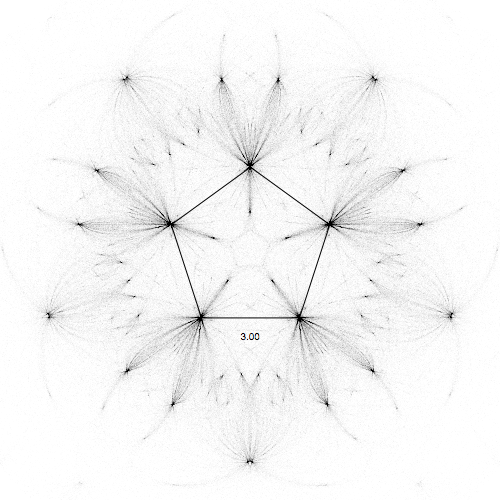
pentagons:
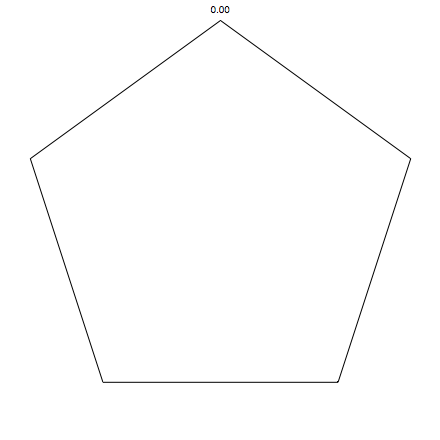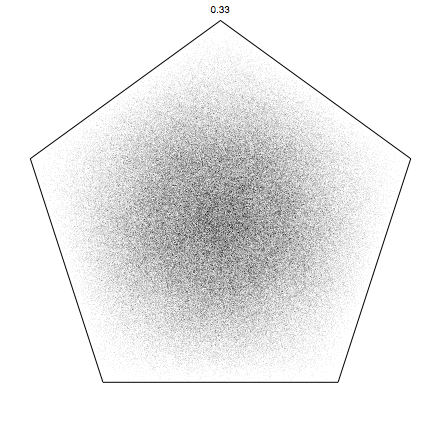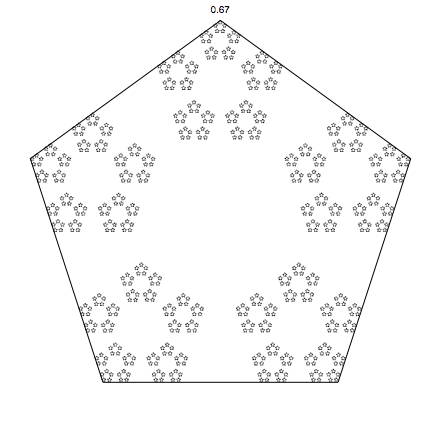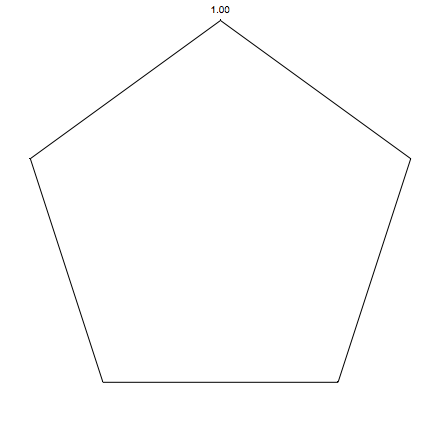
Of course we are not limited by our range 0 to 1, we can go beyond. (negative alpha means you run away, quickly going outside the screen, so that is not a good idea). Here for pentagons, and for alpha up to 1.8:

Distance jumping
Rather than jumping a certain fraction, let's jump a specific distance in the direction of our point. Again we modify the code quite easily:
ClearAll[sequence,DistanceJump]
sequence[n_,m_]:=RandomChoice[Range[n],m]
DistanceJump[n_,m_,d_]:=Module[{circlepoints,seq,pts,counts,img,bg,reg,size},
circlepoints=N@CirclePoints[n];
seq=sequence[n,m];
pts=FoldList[#1+d Normalize[circlepoints[[#2]]-#1]&,First[circlepoints],seq];
size=3;
counts=Transpose@BinCounts[pts,{-size,size,size/250.0},{-size,size,size/250.0}];
counts=Reverse[counts];
reg=Quantile[Join@@counts,0.999];
img=Image[1- counts/reg];
bg=Graphics[Graphics[{FaceForm[],EdgeForm[Black],RegularPolygon[n],Text[NumberForm[d,{\[Infinity],2}],{0,-1.05}]},ImageSize->500,PlotRange->size]];
bg=Rasterize[bg,"Image",RasterSize->ImageDimensions[img],ImageSize->ImageDimensions[img]];
ImageMultiply[img,bg]
]
Let's try it out:
DistanceJump[5, 10^6, 0.5]
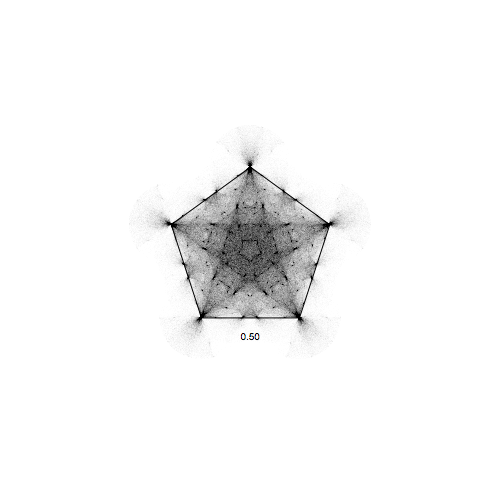
again we see patterns emerge; let's again make a movie varying the distance d:
j=0;
Dynamic[j]
n=3;
CloseKernels[];
LaunchKernels[4];
DistributeDefinitions[DistanceJump,n]
SetSharedVariable[j];
imgs=ParallelTable[j++;DistanceJump[n,10^6,d],{d,0.1,3,0.01}];
Export[ToString[n]<>"distance.gif",imgs,"DisplayDurations"->1/25.0]

and for a pentagon:

Really nice visualization with very complicated patterns emerging from the very simple equations! Hope you enjoyed this little exploration.