I hope this helps, I am rewriting the problem a little bit.
First the list of points:
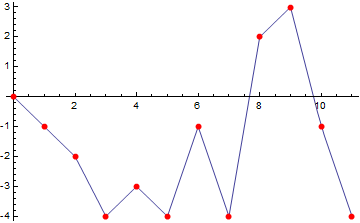
points = {{0, 0}, {1, -1}, {2, -2}, {3, -4}, {4, -3}, {5, -4}, {6, -1}, {7, -4}, {8, 2}, {9, 3}, {10, -1}, {11, -4}};
Next the piecewise linear interpolation function:
f = Interpolation[points, InterpolationOrder -> 1]
Visualize them together in a plot:
Plot[f[x], {x, 0, 11}, Epilog -> {AbsolutePointSize[6], Red, Point[points]}]
Next the 'fg' function:
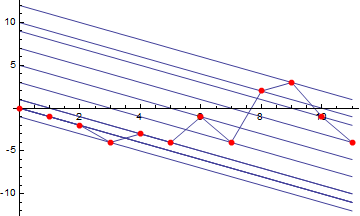
fg[x_, pos_] := -x*Tan[Pi/4] + points[[pos, 2]] + points[[pos, 1]]*Tan[Pi/4]
And visualize again, everything together:
Plot[Join[{f[x]}, Table[fg[x, i], {i, 1, 12}]], {x, 0, 11},
Epilog -> {AbsolutePointSize[6], Red, Point[points]}]
Now solve for one of the intersections:
FindRoot[fg[x, 9] == f[x], {x, 8.5}] (* returns {x->8.} *)