@Isidro Meneses: The simplest way for you (not the fastest for the computer) is probably this:
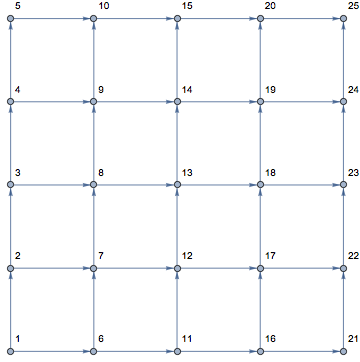
Construct graph and notice the ordering of vertices:
g = GridGraph[{5, 5}, DirectedEdges -> True, VertexLabels -> "Name"]
Enter matrix:
matrix = {{0, 5, 12, 5, 10},
{5, 11, 5, 11, 5},
{10, 5, 0, 5, 15},
{5, 11, 5, 14, 5},
{10, 5, 13, 5, 0}};
Notice that we can get the value of a graph node by using the node name (which is an integer here) to index this vector:
values = Flatten[matrix]
Find all paths from source to sink:
paths = FindPath[g, 1, 25, Infinity, All]
See their sums:
Total@values[[#]] & /@ paths
(*
{53, 54, 54, 55, 55, 54, 54, 55, 55, 43, 44, 44, 44, 44, 45, 55, 55, \
56, 56, 44, 45, 45, 45, 45, 46, 44, 45, 45, 45, 45, 46, 56, 56, 57, \
57, 55, 55, 56, 56, 44, 45, 45, 45, 45, 46, 44, 45, 45, 45, 45, 46, \
56, 56, 57, 57, 45, 46, 46, 46, 46, 47, 57, 57, 58, 58, 57, 57, 58, \
58, 57} *)
None seem to be 51:
Position[%, 51]
(* {} *)
A better way would be to assign the values to the out-edge of each vertex (start with GroupBy[EdgeList[g], First]), then use FindPath[weightedGraph, 1, 25, {51}, All]. This would probably be faster. But it takes longer to program, and since the simple brute-force solution from above runs instantaneously for such a small matrix, there is no point to programming anything more complicated.