Dear Members of the of the community I have written a very simple piece of code to dynamically calculate Fourier coefficients of a signal. The code is something like this

f = 60;
h = 6;(*Harmonic number*)

u1[t_] = Sin[2 \[Pi] f t] + 5 Sin[2 \[Pi] 3 f t] + 
  0.8 Cos[2 \[Pi] 6 f t] + 5;
tau = 1/f;m2 = NDSolve[{
    ff1'[t] == u1[t] Cos[2 \[Pi] 6 f t], ff1[t /; t <= 0] == 0.0,
    f2'[t] == ff1'[t - tau], f2[t /; t <= 0] == 0}, {ff1[t], 
    f2[t]}, {t, 0, 3 tau}];
Plot[Evaluate[{2 f (ff1[t] - f2[t])} /. m2], {t, 0, 3 tau}, 
 PlotRange -> All]

For a signal

u1[t_] = Sin[2 \[Pi] f t] + 5 Sin[2 \[Pi] 3 f t] + 
   0.8 Cos[2 \[Pi] 6 f t] + 5;

The plot would be

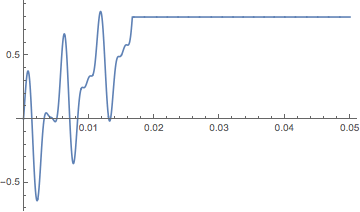
After a transient the output converges to 0.8, that is the coefficient of the sixth harmonic in u[t]. I have try the same defining a model by StateSpaceModel and solving with OutputResponse.

m1 = StateSpaceModel[{ff1'[t] == signal[t] Cos[2 \[Pi] h f t], 
    f2'[t] == ff1'[t - tau]}, {ff1[t], 
    f2[t]}, {signal[t]}, {2 f (ff1[t] - f2[t])}, t];
y1 = OutputResponse[m1, u1[t], {t, 0, 3 tau}];
Plot[y1, {t, 0, 3 tau}]

In such a case the output is .

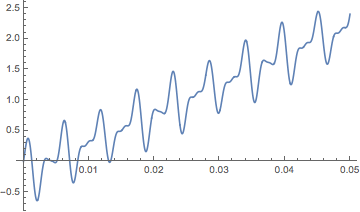
It seems to me that both models are equivalent and should produce same results but they don't!.
Could anybody give a hint on what I am doing wrong?

Cheers Jesus Rico