Hi Bill, can I ask what version of Mathematica you are using? I've copied and pasted the exact same code onto my notebook and am still having the same problem.

Use the option Exclusions -> None to ContourPlot

V[r_, \[CurlyPhi]_] := 
  Exp[-(r - 1)^2]*(Exp[-\[CurlyPhi]^2] + 
      Exp[-(\[CurlyPhi] - 2 \[Pi]/3)^2] + 
      Exp[-(\[CurlyPhi] + 2 \[Pi]/3)^2]) /. \[CurlyPhi] -> 
    ArcTan[x, y];
TransformedField["Polar" -> "Cartesian", 
  V[r, \[CurlyPhi]], {r, \[CurlyPhi]} -> {x, y}];
ContourPlot[%, {x, -2, 2}, {y, -2, 2}, PlotRange -> All, 
 Exclusions -> None]

Good responses all around, and I agree. It's useful to think about the conditions where you expect an inverse function to exist, and how are the inverse functions defined or calculated from first principles?

You should conclude that the notion of an inverse function is essentially a local concept, limited to domains where the direct function is either strictly increasing or strictly decreasing.

Then, if necessary, you can program functionality to "patch" your direct and inverse functions. For example:

Show[
 Plot[Cos[x], {x, -Pi, 0}],
 Plot[Cos[x], {x, 0, Pi}, PlotStyle -> Red], PlotRange -> All,
 ImageSize -> 500
 ]

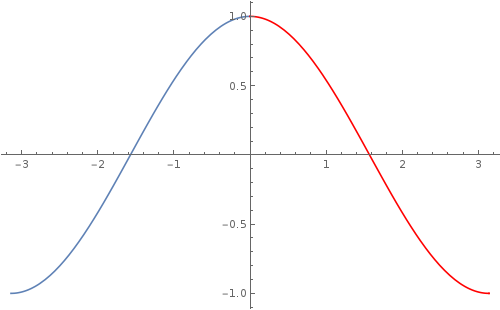
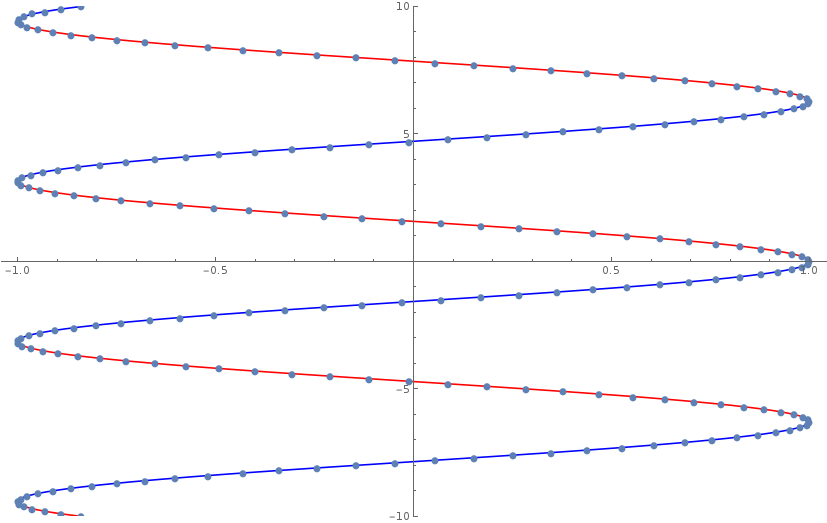
Extrapolate this patching scheme to the entire domain, taking advantage of translation ivariance. Then permute $x$ and $y$ axis, and you will calculate the following patched inverse function

Show[

Plot[
-ArcCos[x] + 2 Pi # & /@ Range[-5, 5], {x, -1, 1}, 
PlotRange -> {-10, 10}, PlotStyle -> Blue],
Plot[
ArcCos[x] + 2 Pi # & /@ Range[-5, 5], {x, -1, 1}, 
PlotRange -> {-10, 10}, PlotStyle -> Red],
ListPlot[{Cos[#], #} & /@ (Range[-150, 100]/10), 
PlotMarkers -> {Automatic, 10}]]

Thanks, Brad.

To put it in simple terms, if ArcCos did not evaluate to a number it would be fairly useless. Same for Log and all the rest.

As for multiple solutions to trig equations, there is Solve and Reduce. Example:

In[203]:= Solve[Cos[x] == 1, x]

(* Out[203]= {{x ->  ConditionalExpression[2 \[Pi] C[1], C[1] \[Element] Integers]}} *)