Main Idea

The main Idea of this project is: Find ways for correcting non-SyntaxQ expressions to SyntaxQ expressions.

As example: we have this string: "Fold[Plus,a,{b,c,d,e}]". We can remove it one character from this string and get aStringLength["Fold[Plus,a,{b,c,d,e}]"]` different strings. We can get it by

inp = "Fold[Plus,a,{b,c,d,e}]";
StringDrop[inp, {#}] & /@ Range[StringLength[inp]]

So, it will 22 different strings:

old[Plus,a,{b,c,d,e}] Fld[Plus,a,{b,c,d,e}] ... Fold[Plus,a,{b,c,d,e] Fold[Plus,a,{b,c,d,e}

Some of them will give us True for function SyntaxQ. Let's try sort it by Select:

dropped = StringDrop[inp, {#}] & /@ Range[StringLength[inp]]
Select[dropped, Not[SyntaxQ[#]] &]

And we got only 4 results from 22:

FoldPlus,a,{b,c,d,e}] Fold[Plus,a,b,c,d,e}] Fold[Plus,a,{b,c,d,e] Fold[Plus,a,{b,c,d,e}

Let's try to evaluate it by function ToExpression.

Map[ToExpression, Select[dropped, Not[SyntaxQ[#]] &]]

And we get list of errors:

{$Failed, $Failed, $Failed, $Failed}

It means that code are not correct, but it will be necessary to check ToExpression on not filtered list of strings:

Map[ToExpression, dropped]

{old[Plus,a,{b,c,d,e}] Fld[Plus,a,{b,c,d,e}] Fod[Plus,a,{b,c,d,e}] Fol[Plus,a,{b,c,d,e}] $Failed lus[lus[lus[lus[a,b],c],d],e] Pus[Pus[Pus[Pus[a,b],c],d],e] Pls[Pls[Pls[Pls[a,b],c],d],e] Plu[Plu[Plu[Plu[a,b],c],d],e] Plusa[Plusa[Plusa[b,c],d],e] b+c+d+e+Null a b+a c+a d+a e $Failed a+c+d+e+Null a+bc+d+e a+b+d+e+Null a+b+cd+e a+b+c+e+Null a+b+c+de a+b+c+d+Null $Failed $Failed

As we see, some of them were evaluated without any errors. It is normal because of old, Fld, Fod, Fol, etc., counts as non defined functions. Null also counts as argument of function. It is the main reason of filtering the dropped list of strings. Next step of this topic is the finding way of correction our strings. So, we must construct the algorithm which will correct all $Failed strings into SyntaxQ forms.

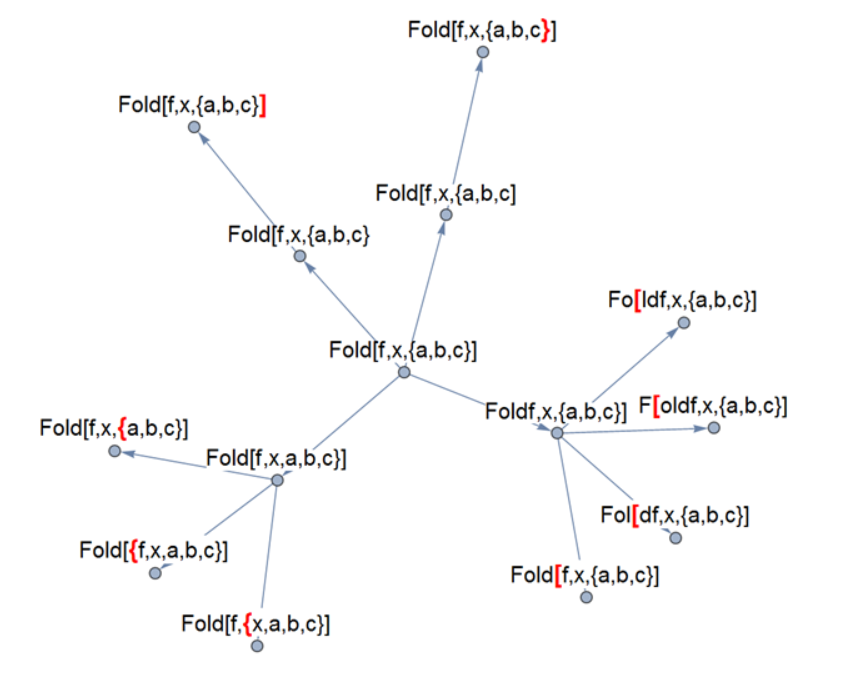
"Intellectual" inserting

The general way to correction is defining of missing character and adding it in every place of our string. Then we must check all our new inputs for Syntax corectness. Inserting of missed character, general way:

correctInserting[str_String, strinst_String] :=
 Module[{s = str, s1, s2, result = {}, i, symb = strinst},
  s1 = StringSplit[str, x : PunctuationCharacter :> x];
  For[
   i = 1, i <= Length[s1], i++,
   If[
    Not[MemberQ[$SystemSymbols, s1[[i]]]],
    s2 =
     {# + Total[StringLength[#] & /@ (s1[[1 ;; i - 1]])],
        StringInsert[s1[[i]], symb, {#}]} &
      /@ Range[StringLength[s1[[i]]] + 1];
    AppendTo[
     result, {s2[[#, 1]], {s1[[1 ;; i - 1]], s2[[#, 2]], 
         s1[[i + 1 ;;]]}} & /@ Range[StringLength[s1[[i]]] + 1]]
    ]
   ];
  DeleteDuplicates[Transpose[{Transpose[Flatten[result, 1]][[1]],
     StringJoin /@ Transpose[Flatten[result, 1]][[2]]}]]

So, this function won't insert character into functions which are in:

Names["System`*"]

First approach

I tried 2 approaches: using of string patterns and using internal service of Mathematica for checking the errors. During my work in WSS2017 I chosed the second way. But let's explain why? The main idea of pattern system was a decomposition of our string into substrings. As example:

Fold[f,x,{1,2,3}] -> {Fold,f,x,{1,2,3}}

Then we check each element by SyntaxQ;

SyntaxQ/@{Fold,f,x,{1,2,3}}

Then we convert a list of boolean values into list of 1 and 0 by Boole.

Boole[SyntaxQ/@{Fold,f,x,{1,2,3}}]

I supposed that a decomposition which have a biggest number in binary representation is right correction of our string. But this way can't maintain all possible variant. Introducing the function equal to Boole but in terms of ternary system or quarternary. I tried to reproduce the ternary equivalent of Boole and it can maintain more kinds of inputs.

But this system have many disadvantages: slow, inefficient, etc.

I will show the last version of string patterns system of this:

brPrSol3[str_String] :=
 Module[{x = str, result},
  fbr =
   FixedPointList[
    StringReplace[
      #,
      x__ ~~ "[" ~~ y__ ~~ "]" ~~ z___ /;
        StringCount[y, "["] == StringCount[y, "]"] &&
         StringCount[x, {"[", "]"}] == 0 &&
         ContainsAny[Names["System`*"], {x}] &&
         StringCount[z, {"[", "]"}] == 0 &&
         commaCounter[x] == 
          StringCount[emptyBracketCollapse@bracesCollapse@y, ","]
       :> y
      ] &,
    str
    ];
  result = Flatten[fbr]
  ]

It worked very slow and always I could give input which would not give me correct output:

Subsets[{a, b, c]

You can look at this pattern system on my GitHub or by this directlink.

Second approach

The second way is using Block construction:

messageAnalysis[str_] :=
  Module[{mess, result},
   Block[{$MessageList = {}},
    Quiet[
     ToExpression[str];
     mess = $MessageList;
     ];
    result = (mess === {})
    ];
   result
   ];

So, If we have any message it will give us False. And this function messageAnalyser allow to analyse all our construction more precisely. You can look at this more here. messageAnalysis allow us to check each results of correctInserting. Then we introduce some filters:

testAnalyser[str_String, initStr_, nulltest_] := 
 messageAnalysis[str] && 
  EditDistance[
    StringDelete[ToString[ToExpression[str], InputForm], 
     WhitespaceCharacter], initStr] >= 
   1 && (StringCount[
      StringDelete[ToString[ToExpression[str], InputForm], 
       WhitespaceCharacter], "Null"] == 0 || Not[nulltest])

By nulltest we can sort result into two piles: Not contains Null and Can contains Null. Also we remove all results which have EditDistance with initial string less than 1. Full code you can look here.

Panel Version

Also we tried to do something like an application for live-correcting input cell:

Panel[
 Style[
  Column[
   {
    InputField[Dynamic[inpstr], String, ContinuousAction -> True],
    Dynamic[Quiet[syntaxCorrector[inpstr]]]
    }
   ], Background -> White
  ]
 ]

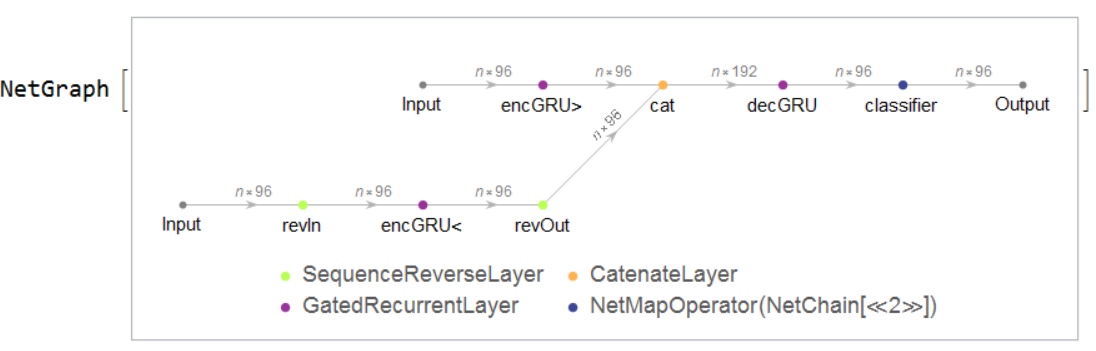
"Prototype" of Neural Net

We built a prototype of neural net, that maybe be able to learn a templates of Wolfram Language. I don't have enought time for immerse myself in the topic of neural networks for finishing this part of WSS project.

validCharacters = StringJoin@CharacterRange[30, 125];
net00 = NetGraph[
  <|
   "revIn" -> SequenceReverseLayer[],
   "encGRU<" -> GatedRecurrentLayer[96],
   "revOut" -> SequenceReverseLayer[],
   "encGRU>" -> GatedRecurrentLayer[96],
   "cat" -> CatenateLayer[2],
   "decGRU" -> GatedRecurrentLayer[96],
   "classifier" -> NetMapOperator[
     NetChain[{LinearLayer[StringLength[validCharacters]], 
       SoftmaxLayer[]}]
     ]
   |>,
  {NetPort["Input"] -> "revIn" -> "encGRU<" -> "revOut", 
   NetPort["Input"] -> "encGRU>", {"revOut", "encGRU>"} -> 
    "cat" -> "decGRU" -> "classifier" }, 
  "Input" -> NetEncoder[{"Characters", validCharacters, "UnitVector"}],
  "Output" -> NetDecoder[{"Characters", validCharacters}]
  ]

Conslusions

• We have a algorithm that can work with all types of string where we can correct it only by adding 1 character.
• We have a prototype of neural net and dataset for it.

Future directions

• Complete the neural net.
• Introduce the new features in algorithm.
• Improve algorithm by adding a possibility to add in string 2 or more additional characters.