Just a tiny little more info. In case that you need other color schemes for actual spectrum with physical meaning, you can go to the menu bar and click "Palettes" -> "Color Scheme" ->"Physical " -> "Visible spectrum". You can see that the default range for this color data is not from 0 to 1 but from 380 to 750, which corresponding to the physical wave length.
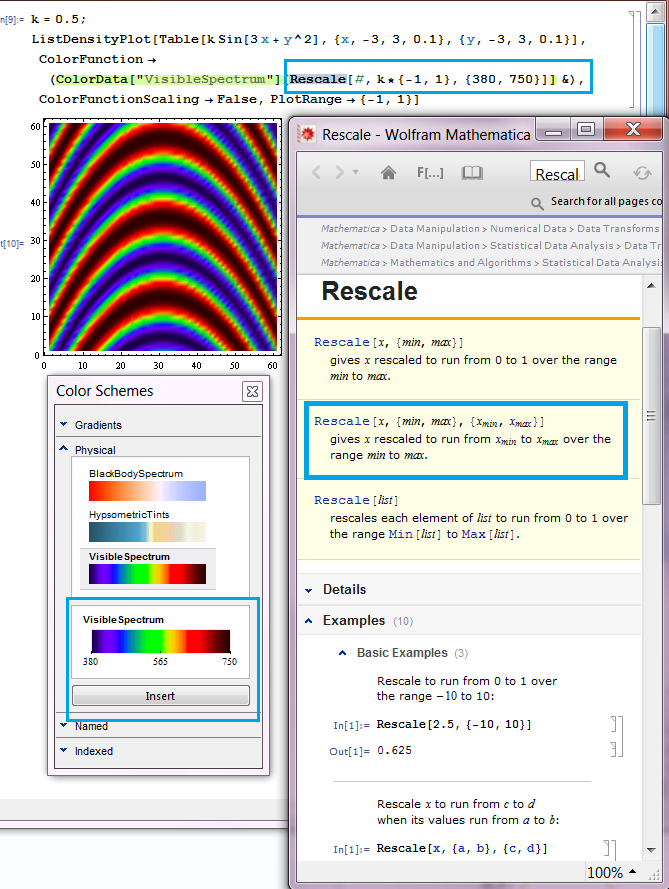
Thus you just need to add a color range in to the Rescale function and it will convert the range of your function to that of the visible spectrum. This is very handy extension to the default cases above. Here is the workable code:
k = 0.5;
ListDensityPlot[
Table[k Sin[3 x + y^2], {x, -3, 3, 0.1}, {y, -3, 3, 0.1}],
ColorFunction -> (ColorData["VisibleSpectrum"][
Rescale[#, k*{-1, 1}, {380, 750}]] &),
ColorFunctionScaling -> False, PlotRange -> {-1, 1}]