Background
I am reading "Introductory Combinatorics" by Brualdi. In Chapter 4, an algorithm is introduced to generate all permutations of a list of number $\{1,2,3,...,n\}$. In the case of four elements, according to the book, the order of permutation looks like the following:

Brualdi use an algorithm introduced mentioned by S. Even to implement the interlaced pattern:

I think it would fun to animate this process in Wolfram Language. Notice the how the numbers and arrow direction are updated:
Animation of 4 elements
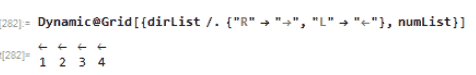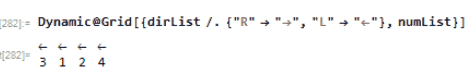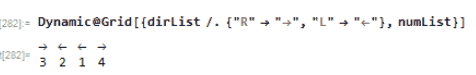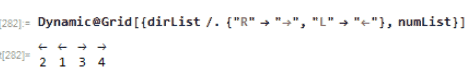
Animation with 5 elements. Cure to insomnia

A notebook which contains all running code is attached. Please find it at the end of this thread.
Explanation
To implement this algorithm, we introduce
Number-direction pair. For example 2 is with an arrow atop which pointing to the right ;1 is with an arrow atop which pointing to the left
dirList={"R","R","R","L","R","R"};
numList={2,6,3,1,5,4};
Mobile Integer. In the list above, $6$, $3$ and $5$ are mobile integers because the arrow of each item points to a smaller number than itself. $6$ with "R", means $6$ looks toward right at $3$, and $6>3$. Apparently 2 is not a mobile integer since 2 is less 6 which is on the right side. So is not 1, which is never a mobile integer. 4 is not mobile integer because there is no element on the right hand side of itself. The following code checks whether kth item in a list is a mobile integer or not:
mobileIntQ[numList_List,dirList_List,kth_Integer]:=With[{max=Length[numList],newposition=If[dirList[[kth]]=="R",kth+1,kth-1]},
Which[
newposition>max || newposition==0,False,
numList[[kth]]> numList[[newposition]],True,
True,False
]
]
(* Test *)
In[310]:= Cases[Range[6],x_/;mobileIntQ[numList,dirList,x]]
(*the 2nd, 3rd and 5th items are mobile integers*)
Out[310]= {2,3,5}
In[311]:= numList[[%]]
Out[311]= {6,3,5}
The algorithm
- Start with {1,2,...,n} and {L,L,L,...,L},
- Determine the largest mobile integer k
- Move the largest one only in the next step following the direction of its arrow
- Flip the direction of all integers p in the list with p > k
- Do the last four steps again and again. Terminate until no mobile integer is found in the list.
Here is a step-by-step implementation. Suppose we have 4 elements
(*initialization*)
itemsNum = 4;
numList = range = Range[itemsNum];
dirList = ConstantArray["L", itemsNum];
(* define direction flip actions *)
flipDir["L"] = "R";
flipDir["R"] = "L";
find out if the nth item in the list is mobile/Pickout the largest
mobileIndex = Cases[range, x_ /; mobileIntQ[numList, dirList, x]] (* => {2, 3, 4}*)
mobileInts = numList[[mobileIndex]] (* => {2, 3, 4} *)
Here we find k=4 at position 4th (right most of the number list)
target = SortBy[Thread[mobileInts -> mobileIndex], First] // Last (* => 4 -> 4*)
Move 4 to the left for one step or just swap the position of 3 and 4:
maxMobileInt = target[[1]];
pos = target[[2]];
next = If[dirList[[pos]] == "R", pos + 1, pos - 1];
dirList[[{pos, next}]] = dirList[[{next, pos}]];
numList[[{pos, next}]] = numList[[{next, pos}]];
By the third step, flip the items in the number list that are larger than k = 4 (since no item is larger than 4, the direction list seems untouched):
With[{flip = Cases[numList, x_ /; x > maxMobileInt]},
If[flip != {},
toBeFlipped = Position[numList, #][[1, 1]] & /@ flip;
dirList[[toBeFlipped]] = flipDir /@ dirList[[toBeFlipped]];,
Clear[toBeFlipped]]
]
Till now we finished the first move:
numList = {1,2,3,4} = > numList = {1,2,4,3} , dirList = {L, L, L, L} => {L, L, L, L}
The non-trivial move is the following:
{4,1,2,3} = > {4,1,3,2} , {L, L, L, L} => {R, L, L, L}
{4,1,3,2} = > {1,4,3,2} , {R, L, L, L} => {L, R, L, L}
Notice when
numList={4,1,2,3};
mobileIndex=Cases[range,x_/;mobileIntQ[numList,dirList,x]] (* *)
(* {3,4} = third and fourth element in numList are mobile integer *)
the leading 4 in numList with L is no longer a mobile integer and the largest mobile integer in the updated numList is 3. At this moment toBeFlipped is, for the first time, assigned value 1, which is position of 4 in numList. Thus the direction list dirlist changes from {L,L,L,L} to {R,L,L,L}.
The next move is obvious because in {4,1,3,2} with {R, L, L, L} 4 is the largest mobile integer to move right-ward. Therefore we have a switching point of 4 on the interlaced path:
1,4,2,3
4,1,2,3
4,1,3,2
1,4,3,2
Once we learn how this transition point is achieved by the code above, the rest part of the interlace pattern follows naturally.
 Attachments:
Attachments: