I have a suspicion something is funky with the symbolic solution to the inner sum that produces the Hypergeometric1F1. 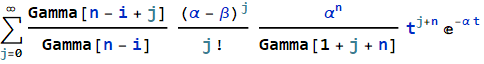
When you use Set to define Pmoe, then Simplify[Pmoe1[A, \[Alpha], \[Beta], t, 1] == Pmoe2[A, \[Alpha], \[Beta], t, n] /. n -> 1] is True, but neither equals Pmoe2[A, \[Alpha], \[Beta], t, 1] that has already had the symbolic sum taken. On the other hand, using SetDelayed to define Pmoe we have Simplify[Pmoe1[A, \[Alpha], \[Beta], t, 1] == Pmoe2[A, \[Alpha], \[Beta], t, 1]] is True, but neither equals Pmoe2[A, \[Alpha], \[Beta], t, n] /. n -> 1. I think this means there is agreement only when the inner sum is either taken first or not taken first, but I am honestly a bit confused here.