Group Abstract Group Abstract

Message Boards Message Boards

0
|
12.7K Views
|
4 Replies
|
1 Total Like
View groups...
Share
Share this post:

Summations on the same expression do not give the same result?

Zhehao Zhang
Posted 8 years ago

Hey guys:

When I tried to take summation with respect to my expression Pmoe, I found that the Mathematica does not give consistent results if I put the summation symbol in different places. Please see my attachment where I use Pmoe1 and Pmoe2 to represent two different ways of summation, which should give the same result. It turns out that Pmoe1 is correct if you let Mathematica give values for each i and then sum all the values up. Appreciate anyone who can explain it a bit more.

Thanks in advance.

Attachments:
POSTED BY: Zhehao Zhang
4 Replies
Sort By:
Zhehao Zhang
Zhehao Zhang
Posted 8 years ago

Hey Kyle, actually, my question is exactly from your concern. Please check the attachment.

I also met another case where one expression is in the integral form while the other one is in the summation form. The numerical results do not correspond while those two expression equal in theoretical sense. I report to the Wolfram one month ago and have not received any responses yet. Here is the link http://community.wolfram.com/groups/-/m/t/1167817?p_p_auth=65adeLkN

Again, I tried to increase the accuracy level, with precision up to 700, while no thing changes..

Attachments:
POSTED BY: Zhehao Zhang

I have a suspicion something is funky with the symbolic solution to the inner sum that produces the Hypergeometric1F1. 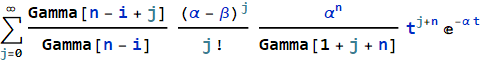Symbolic sum that might be causing issue

When you use Set to define Pmoe, then Simplify[Pmoe1[A, \[Alpha], \[Beta], t, 1] == Pmoe2[A, \[Alpha], \[Beta], t, n] /. n -> 1] is True, but neither equals Pmoe2[A, \[Alpha], \[Beta], t, 1] that has already had the symbolic sum taken. On the other hand, using SetDelayed to define Pmoe we have Simplify[Pmoe1[A, \[Alpha], \[Beta], t, 1] == Pmoe2[A, \[Alpha], \[Beta], t, 1]] is True, but neither equals Pmoe2[A, \[Alpha], \[Beta], t, n] /. n -> 1. I think this means there is agreement only when the inner sum is either taken first or not taken first, but I am honestly a bit confused here.

POSTED BY: Kyle Keane
Zhehao Zhang
Zhehao Zhang
Posted 8 years ago

Sorry I am not convinced.

My question is why Pmoe1 and Pmoe2 are different, which are both defined by :=.

My understanding for := is that the expression is evaluated on request and for = is that the expression is evaluated immediately. However, Pmoe1 and Pmoe2 equal in theoretical sense, which imply they have the values no matter when they are evaluated.

I also tried to increase the precision level and the result do not change.
POSTED BY: Zhehao Zhang
Bill Simpson
Bill Simpson
Posted 8 years ago

In your definition of Pmoe if you change = to := then the results of the two tables are identical.

If you study the help pages for = and := then perhaps this will help you begin to understand the difference.

The difference in your example depends on when the right hand side of Pmoe will be evaluated.
POSTED BY: Bill Simpson
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard