Message Boards Message Boards

Predicting Winning Odds of Italian Serie A Soccer 1934-2017

Dear Community! Although gambling is not my hobby, the validation of predictor engine inside Wolfram Mathematica 11.2 is. Sooner or later someone may get huge benefits in gambling using predictors as they have been developed already today. I got LaLiga "Outcomes" 100 % but my example will be Italian Serie A analysis, yrs 1934-2017. It is downloadable from

https://github.com/jalapic/engsoccerdata

Note that the source was found by google'ing. I am avoiding to be too lengthy and therefore only minimum amount of outputs are given. For necessary prediction only goals and dates are needed. I have always wondered whether it is useful to put into prediction as much statistical data as possible and it turns out that this must be avoided i.e. the right data for right prediction should be selected for best results. The CSV file should be first downloaded and a little-bit modified in order to use it as Mher Davtyan used it in his original example:

http://community.wolfram.com/groups/-/m/t/908804

then the path may be seen from the import function below:

oddsData = 
 SemanticImport[
  "C:\\Users\\user\\Documents\\engsoccerdata-master\\data-raw\\italy3.\
csv", <|1 -> "Integer", 2 -> "String", 3 -> "Integer", 4 -> "String", 
   5 -> "String", 7 -> Automatic, 8 -> Automatic|>]

giving an output:

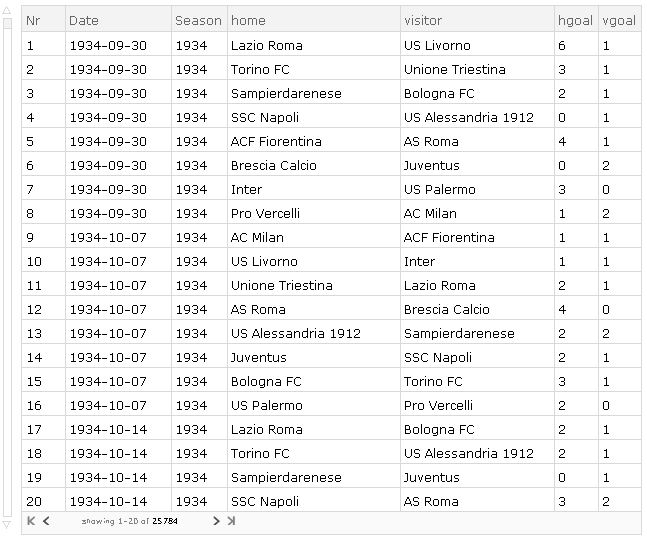
Input data

Yes, it consists of 25784 games. The collection of additions to Dataset are listed below and explained later:

scoreAdded = 
 oddsData[All, 
  Append[#, 
    "Score" -> 
     ToString[Slot["hgoal"]] <> ":" <> ToString[Slot["vgoal"]]] &]

homeAndAway = 
  scoreAdded[
   Association["Home" -> GroupBy[#home &], 
    "Away" -> GroupBy[#visitor &]]];
data01 = (Flatten[(Transpose[{homeAndAway["Home", 
               scoreAdded[#]["home"], All, "Nr"] // Normal, 
             Thread[Rule[
               homeAndAway["Home", scoreAdded[#]["home"], All, 
                 "home"] // Normal, 
               homeAndAway["Home", scoreAdded[#]["home"], All, 
                  "hgoal"] // Normal // Accumulate]]}] & /@ 
          Range[1, 25784, 1]) // Union, 1] // Sort)[[All, 2]][[All, 
   2]];
data02 = (Flatten[(Transpose[{homeAndAway["Away", 
               scoreAdded[#]["visitor"], All, "Nr"] // Normal, 
             Thread[Rule[
               homeAndAway["Away", scoreAdded[#]["visitor"], All, 
                 "visitor"] // Normal, 
               homeAndAway["Away", scoreAdded[#]["visitor"], All, 
                  "vgoal"] // Normal // Accumulate]]}] & /@ 
          Range[1, 25784, 1]) // Union, 1] // Sort)[[All, 2]][[All, 
   2]];
data03 = (Flatten[(Transpose[{homeAndAway["Away", 
               scoreAdded[#]["visitor"], All, "Nr"] // Normal, 
             Thread[Rule[
               homeAndAway["Away", scoreAdded[#]["visitor"], All, 
                 "visitor"] // Normal, 
               homeAndAway["Away", scoreAdded[#]["visitor"], All, 
                  "hgoal"] // Normal // Accumulate]]}] & /@ 
          Range[1, 25784, 1]) // Union, 1] // Sort)[[All, 2]][[All, 
    2]];
data04 = (Flatten[(Transpose[{homeAndAway["Home", 
               scoreAdded[#]["home"], All, "Nr"] // Normal, 
             Thread[Rule[
               homeAndAway["Home", scoreAdded[#]["home"], All, 
                 "home"] // Normal, 
               homeAndAway["Home", scoreAdded[#]["home"], All, 
                  "vgoal"] // Normal // Accumulate]]}] & /@ 
          Range[1, 25784, 1]) // Union, 1] // Sort)[[All, 2]][[All, 
    2]];
addIndividualGoalsCumul[d_] := 
  Join[d, Association["homeTeamHomeRating" -> (data01[[d["Nr"]]]), 
    "VisitorAwayRating" -> (data02[[d["Nr"]]]), 
    "homeTeamHomeConceded" -> (data04[[d["Nr"]]]), 
    "VisitorAwayConceded" -> (data03[[d["Nr"]]])]];

ratingsAdded = Map[addIndividualGoalsCumul[#] &, scoreAdded]
extractDate[a_] := 
 Append[a, <|
   "DateSuccessive" -> 
    FromDigits[StringSplit[a["Date"], "-"][[1]]] 100 - 190000 + 
     FromDigits[StringSplit[a["Date"], "-"][[2]]]|>]
dateNew = Map[extractDate[#] &, ratingsAdded]
addOutcome[a_Association] := 
 If[a["hgoal"] == a["vgoal"], Append[a, Association["Outcome" -> 0]], 
  If[a["hgoal"] > a["vgoal"], Append[a, Association["Outcome" -> 1]], 
   Append[a, Association["Outcome" -> -1]]]]

outcomeAdded = Map[addOutcome[#] &, dateNew]

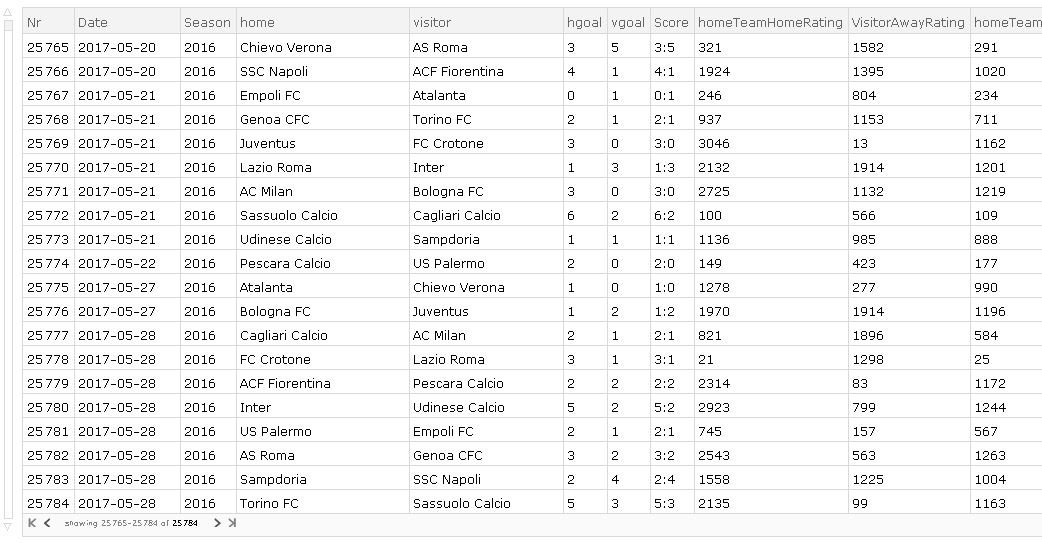
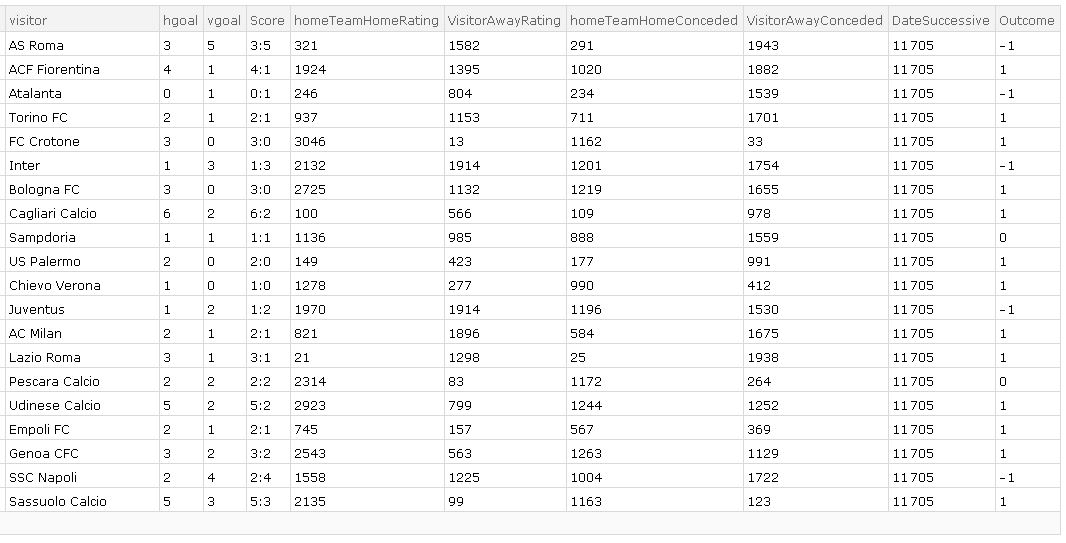
where data01, data02, data03 and data04 compute the cumulative scores and conceded scores for every team, the "DateSuccessive" modifies the "Date": 1934-06-23 to 03406 and 2017-05-28 to 11705 i.e. year and month, and "Outcome" is similar as in original post. The result table is: Final Dataset 1 Final Dataset 2

The test data starts from index:

In[96]:= Round[0.99218 Length[outcomeAdded]]

Out[96]= 25582

and consists of all 202 games played on yr 2017 for test set for Classifier: 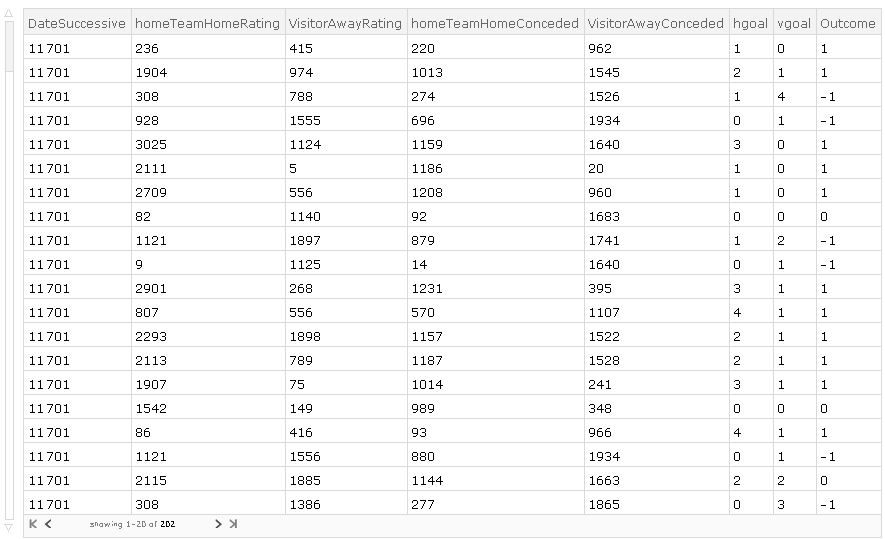Testset Above we see the Testset and needed data using the code:

n = Round[0.99218 Length[outcomeAdded]];

{trainingSet, testSet} = 
  TakeDrop[outcomeAdded[
    All, {"DateSuccessive", "homeTeamHomeRating", "VisitorAwayRating",
      "homeTeamHomeConceded", "VisitorAwayConceded", "hgoal", "vgoal",
      "Outcome"}], n];

c = Classify[trainingSet -> "Outcome", Method -> "LogisticRegression"]  cm = ClassifierMeasurements[c, testSet -> "Outcome"]

with following results:

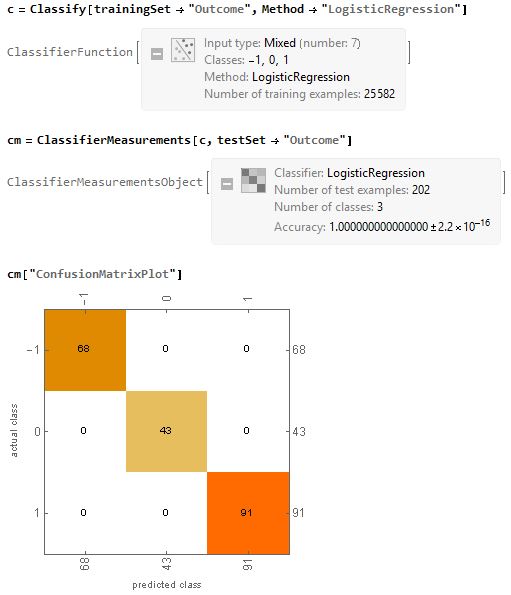
enter image description here

Visualisation:

In[138]:= actaulValue = testSet[All, "Outcome"] // Normal

Out[138]= {1, 1, -1, -1, 1, 1, 1, 0, -1, -1, 1, 1, 1, 1, 1, 0, 1, -1, \
0, -1, -1, 1, 1, 1, 0, 1, -1, -1, 1, 1, -1, 0, 1, 0, 0, 1, -1, 0, 1, \
-1, -1, 1, 0, 0, -1, 1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, -1, 1, \
-1, 1, 0, 1, 1, -1, -1, -1, 1, 1, 1, 0, -1, 1, -1, 1, -1, 0, -1, 1, \
0, -1, 0, 1, -1, 1, 0, -1, -1, 0, -1, 1, 0, 1, -1, 1, 1, 1, 1, -1, \
-1, -1, 1, 1, 0, 1, 1, 0, -1, -1, 1, -1, 1, 1, -1, -1, 1, -1, 0, -1, \
0, 0, -1, 0, 0, 1, -1, -1, 1, -1, 1, 0, 1, 1, -1, 0, 0, 1, 0, -1, 0, \
1, 0, 1, 1, -1, 1, 1, -1, -1, 0, 1, -1, 0, 0, 1, 1, 0, -1, -1, -1, 1, \
-1, 0, 1, 0, 1, 1, 1, -1, -1, 0, 0, 0, 1, 1, 1, 1, -1, 1, 1, 0, -1, \
-1, 1, -1, 1, 1, -1, 1, 1, 0, 1, 1, -1, 1, 1, 0, 1, 1, 1, -1, 1}

In[139]:= predictedValue = 
 c[Normal[testSet[[All, Values]]][[All, ;; 7]]]

Out[139]= {1, 1, -1, -1, 1, 1, 1, 0, -1, -1, 1, 1, 1, 1, 1, 0, 1, -1, \
0, -1, -1, 1, 1, 1, 0, 1, -1, -1, 1, 1, -1, 0, 1, 0, 0, 1, -1, 0, 1, \
-1, -1, 1, 0, 0, -1, 1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, -1, 1, \
-1, 1, 0, 1, 1, -1, -1, -1, 1, 1, 1, 0, -1, 1, -1, 1, -1, 0, -1, 1, \
0, -1, 0, 1, -1, 1, 0, -1, -1, 0, -1, 1, 0, 1, -1, 1, 1, 1, 1, -1, \
-1, -1, 1, 1, 0, 1, 1, 0, -1, -1, 1, -1, 1, 1, -1, -1, 1, -1, 0, -1, \
0, 0, -1, 0, 0, 1, -1, -1, 1, -1, 1, 0, 1, 1, -1, 0, 0, 1, 0, -1, 0, \
1, 0, 1, 1, -1, 1, 1, -1, -1, 0, 1, -1, 0, 0, 1, 1, 0, -1, -1, -1, 1, \
-1, 0, 1, 0, 1, 1, 1, -1, -1, 0, 0, 0, 1, 1, 1, 1, -1, 1, 1, 0, -1, \
-1, 1, -1, 1, 1, -1, 1, 1, 0, 1, 1, -1, 1, 1, 0, 1, 1, 1, -1, 1}

In[140]:= difference = actaulValue - predictedValue

Out[140]= {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}

In[141]:= N@Normalize[Counts[Abs[difference]], Total]

Out[141]= <|0 -> 1.|>

Concluding that all yr 2017 game winners were correctly classified. Now, prediction with slightly larger set:

In[143]:= n = Round[0.99 Length[outcomeAdded]]

Out[143]= 25526

In[144]:= {trainingSetFull, testSetFull} = TakeDrop[outcomeAdded, n];

{trainingSet1, 
   testSet1} = {trainingSetFull[
    All, {"DateSuccessive", "homeTeamHomeRating", "VisitorAwayRating",
      "homeTeamHomeConceded", "VisitorAwayConceded", "hgoal", "vgoal",
      "Outcome"}], 
   testSetFull[
    All, {"DateSuccessive", "homeTeamHomeRating", "VisitorAwayRating",
      "homeTeamHomeConceded", "VisitorAwayConceded", "hgoal", "vgoal",
      "Outcome"}]};

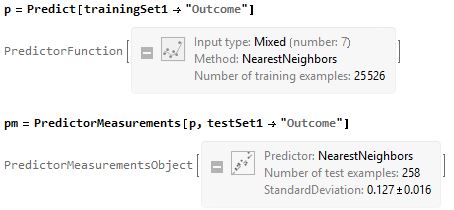
enter image description here

In[156]:= predictedValue = 
 Round[p[Normal[testSet1[[All, Values]]][[All, ;; 7]]], 1]

Out[156]= {1, 1, -1, -1, 1, 0, 1, -1, 1, -1, 1, 0, 1, -1, 1, 1, 0, 1, \
1, 1, -1, 1, 0, 1, 1, 0, 1, 1, -1, -1, 0, -1, 1, -1, -1, 1, 1, 1, 1, \
1, 0, 1, 0, 1, 1, -1, -1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, -1, -1, 1, \
1, 1, 0, -1, -1, 1, 1, 1, 1, 1, 0, 1, -1, 0, -1, -1, 1, 1, 1, 0, 1, \
0, -1, 1, 1, -1, 0, 1, 0, 0, 0, -1, 0, 1, -1, -1, 1, 0, 0, -1, 1, -1, \
1, -1, 1, -1, -1, 1, 1, -1, -1, 1, -1, 1, -1, 1, 0, 1, 1, -1, -1, -1, \
1, 1, 1, 0, -1, 1, -1, 1, -1, 0, -1, 1, 0, -1, 0, 1, -1, 1, 0, -1, \
-1, 0, -1, 1, 0, 1, -1, 1, 1, 1, 1, -1, -1, -1, 1, 1, 0, 1, 1, 0, -1, \
-1, 1, -1, 1, 1, -1, -1, 1, -1, 0, -1, 0, 0, -1, 0, 0, 1, -1, -1, 1, \
-1, 1, 0, 1, 1, -1, 0, 0, 1, 0, -1, 0, 1, 0, 1, 0, -1, 1, 1, -1, -1, \
0, 1, -1, 0, 0, 1, 1, 0, -1, -1, -1, 1, -1, 0, 1, 0, 1, 1, 1, -1, -1, \
0, 0, 0, 1, 1, 1, 1, -1, 1, 1, 0, -1, -1, 1, -1, 1, 1, -1, 1, 1, 0, \
1, 1, -1, 0, 1, 0, 1, 1, 1, -1, 1}

In[157]:= actaulValue = testSet1[All, "Outcome"] // Normal

Out[157]= {1, 1, -1, -1, 1, 0, 1, -1, 1, -1, 1, 0, 1, -1, 1, 1, 0, 1, \
1, 1, -1, 1, 0, 1, 1, 0, 1, 1, -1, -1, 0, -1, 1, -1, -1, 1, 1, 1, 1, \
1, 0, 1, -1, 1, 1, -1, -1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, -1, -1, \
1, 1, 1, 0, -1, -1, 1, 1, 1, 1, 1, 0, 1, -1, 0, -1, -1, 1, 1, 1, 0, \
1, -1, -1, 1, 1, -1, 0, 1, 0, 0, 1, -1, 0, 1, -1, -1, 1, 0, 0, -1, 1, \
-1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, -1, 1, -1, 1, 0, 1, 1, -1, -1, \
-1, 1, 1, 1, 0, -1, 1, -1, 1, -1, 0, -1, 1, 0, -1, 0, 1, -1, 1, 0, \
-1, -1, 0, -1, 1, 0, 1, -1, 1, 1, 1, 1, -1, -1, -1, 1, 1, 0, 1, 1, 0, \
-1, -1, 1, -1, 1, 1, -1, -1, 1, -1, 0, -1, 0, 0, -1, 0, 0, 1, -1, -1, \
1, -1, 1, 0, 1, 1, -1, 0, 0, 1, 0, -1, 0, 1, 0, 1, 1, -1, 1, 1, -1, \
-1, 0, 1, -1, 0, 0, 1, 1, 0, -1, -1, -1, 1, -1, 0, 1, 0, 1, 1, 1, -1, \
-1, 0, 0, 0, 1, 1, 1, 1, -1, 1, 1, 0, -1, -1, 1, -1, 1, 1, -1, 1, 1, \
0, 1, 1, -1, 1, 1, 0, 1, 1, 1, -1, 1}

In[158]:= difference = Round[actaulValue - predictedValue, 0.01]

Out[158]= {0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -1., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
-1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., \
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., \
0., 0., 0., 0., 0., 0.}

In[159]:= N@Normalize[Counts[Abs[difference]], Total]

Out[159]= <|0. -> 0.98062, 1. -> 0.0193798|>

showing 98 % accuracy.

10 Random Samples

randomMatches = RandomSample[testSetFull, 10]

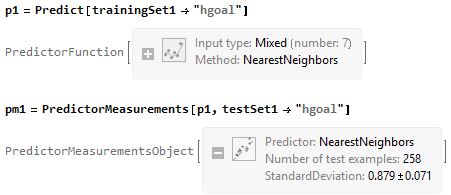
enter image description here Goals prediction is not so exact:

enter image description here

and for visiting team:

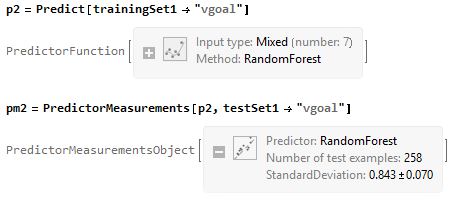
enter image description here
giving 60 % of accuracy.

Having "Outcome" correct, I will just show two tables of Predicted and Actual scores: 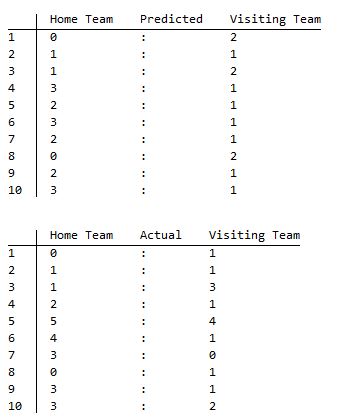enter image description here

Conclusions

Clearly, game scores are harder to predict, almost 60 % are correct and 38 % differs with 1 goal. The predictor seems to work better when adding time-scale. Over the time the team's performance is changing and this must be reflected.

POSTED BY: Tanel Telliskivi
5 Replies
Sort By:
Attachments:
POSTED BY: Tanel Telliskivi
Edson Ferreira
Edson Ferreira
Posted 7 years ago

Summing up For & Against goals (separately) when a team plays as home team or visitor is a interesting approach! I'm very curious to see how would be the results with the corrections mentioned is the comments above!
POSTED BY: Edson Ferreira

Hi, nice post. However, I guess something's wrong. Please correct me if I got it wrong. You are training the classifier by providing the home and away goals. In addition, home goals and away goals are also present in your test set as predictor variables. So, basically you are trying to predict something that you already know.
POSTED BY: Mher Davtyan

enter image description here - Congratulations! This post is now a Staff Pick as distinguished by a badge on your profile! Thank you, keep it coming!

POSTED BY: EDITORIAL BOARD
Edson Ferreira
Edson Ferreira
Posted 7 years ago

Are you using "hgoal" and "vgoal" as predictor variables for "Outcome"?
POSTED BY: Edson Ferreira
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract