Message Boards Message Boards

[?] Manipulate a dynamicly generated expression?

zare bozas
Posted 6 years ago

Hello I wrote some code to calculate and demonstrate robotic like vectors. My functions allow to add vectors and links (changes from coordinate systems from elements) . So I can define the System with Rotation Matrices and vectors and creates a list of Vectors, dependend the los current angeles of the rotations. 

data = {};
angles = {};

Move[vec_] := Module[{},
  (*Move existing vectors to new Position*)
  move[dat_] := {dat[[1]] + vec, dat[[2]] + vec };
   For[i = 1, i <= Length[data], i++, data[[i]] = move[data[[i]]] ];
  (*Print["moved: ",data//MatrixForm];*)
  ]

AddVector[vec_] := AppendTo[data, {{0, 0, 0}, vec}];
AddLink[vec_, rot_, angle_] := Module[{},
   AddRot[rot, angle];
   Move[vec]; 
   AddVector[vec];
   ];
AddRot[rot_, angle_] := Module[{},
   AppendTo[angles, angle];
   (*Print[data//MatrixForm];*)
   AddVector[{0.1, 0, 0}];
   AddVector[{0, 0.1, 0}];
   AddVector[{0, 0, 0.1}];
   (*Print[data//MatrixForm];*)

   (*Alle vektoren im K-System rotieren*)
   (*Print["Rotating Vectors"];*)
   conv[dat_] := {rot[angle].(dat[[1]]), rot[angle].(dat[[2]]) };
    For[i = 1, i <= Length[data], i++, data[[i]] = conv[data[[i]]] ];
   (*Print["rotated: ",data//MatrixForm];*)

   ];

ShowAll[] := Module[{},
  arrows = Arrow[data];
  region = 
   Point[{{0, 0, 2}, {0, 0, -2}, {0, 2, 0}, {2, 0, 0}, {0, -2, 
      0}, {-2, 0, 0}}];
  Print[Graphics3D[{arrows, region}, Axes -> True, ViewPoint -> Front]]
  ]


Ri1[q1_] := ( {
    {Cos[q1], 0, -Sin[q1]},
    {0, 1, 0},
    {Sin[q1], 0, Cos[q1]}
   } );

AddVector[{1, 0, 0}];

AddLink[{1, 1, 1}, Ri1, x];
data // MatrixForm
ShowAll[];

Output:

Output

When I set x to a value, y can display the result en this form:

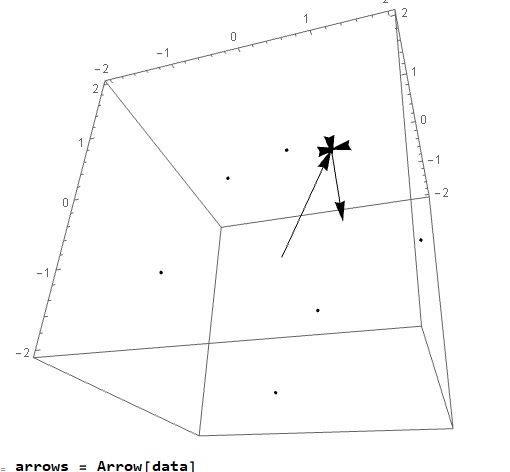
system

My problem is, that i dont know how to put the system to the Manipulate function. I tried something like this, but the amount of variables is not defined:

arrows = Arrow[data]
region = Point[{{0, 0, 2}, {0, 0, -2}, {0, 2, 0}, {2, 0, 0}, {0, -2, 
    0}, {-2, 0, 0}}]
(*parameter  = {Graphics3D[{arrows,region}, Axes -> True,ViewPoint\
\[Rule]Front],Axes -> True,ViewPoint\[Rule]Front};
For[i= 1,i<=Length[angles],i++,AppendTo[parameter,{angles[[i]],0,Pi}];\
*)
 y = Dynamic[
  Graphics3D[{arrows, region}, Axes -> True, ViewPoint -> Front]]
Manipulate[y, {x, 0, Pi}]

Any Ideas how to Manipulate this?
POSTED BY: zare bozas
5 Replies
Sort By:

Zare,

Your arrows are functions of x so you need to pass the variable x to your arrows and manipulate x. Do this instead of ShowAll[]:

Module[{}, arrows[x_] = Arrow[data];
 region = 
  Point[{{0, 0, 2}, {0, 0, -2}, {0, 2, 0}, {2, 0, 0}, {0, -2, 0}, {-2,
      0, 0}}]; 
 Manipulate[
  Graphics3D[{arrows[x], region}, Axes -> True, 
   ViewPoint -> Front], {x, 0, 100}]]

Also, you should not use capital letters for your functions because they will inevitably conflict with internal Mathematica functions/Symbols.

Regards,

Neil
POSTED BY: Neil Singer
zare bozas
zare bozas
Posted 6 years ago

Yes, I know that the arrow is a function of x, but only in this example. I d like to write a universal function, which also allows 2, 3 or more Links. In that cases they would be 2 or 3 parameters. Also i will have the same error which I had already before:

"Tag Arrow in Arrow[{{{1,1,............ ........}}}][x_] is Protected"
POSTED BY: zare bozas

Zare,

Your error is because you need to quit the kernel. You defined arrows one way and I changed the way it is used in the posted code. The code I posted works with your example if you delete ShowAll code and use what I posted instead.

Regards
POSTED BY: Neil Singer
zare bozas
zare bozas
Posted 6 years ago

Thanks,

Yes, it works for me too now. I have 2 questions more:

  1. Why dont you use := for the assignment of the variable "arrow" with parameter?
  2. Like already asked in the first post: Is there a posibility to pass an dynamic count of parameters to the Manipulate function based at the "angles" variable?

Regards
POSTED BY: zare bozas

Zare,

  1. Either are ok in this case, however, Sometimes you evaluate an expression that contains a variable, ie "x". and then want to create a function of x from the evaluated expression, you would use = if you want to evaluate the expression immediately.

  2. You need to be a bit clever to do the dynamic number of parameters to Manipulate. Here is an example that creates at list of the variables in an expression (data) and then constructs the Manipulate that you want.

Lets create a function to get all the variables in an expression:

findAllVars[eqns_] := 
 DeleteCases[
  Union[Flatten[
    Replace[eqns , head_[args___] -> List[args], {0, Infinity}]]], 
  x_ /; NumericQ[x]]

Now we can use it in your example. I assume that "data" contains your expression -- you can also make this a function of data instead of having data being global.

With[{arr = Arrow[data], 
  varSliders = Sequence @@ Map[{#, 0, 100} &, findAllVars[data]]}, 
 Manipulate[
  Graphics3D[{arr, region}, Axes -> True, ViewPoint -> Front], 
  varSliders]]

You need a "With" to place the arrow expression into the Manipulate because Manipulate has attribute HoldAll. You need to construct a sequence to specify the slider variables to the Manipulate. Again, you need to insert the sequence using With. The Map constructs the arguments in the proper format for Manipulate.

I hope this helps.

Regards,

Neil
POSTED BY: Neil Singer
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract