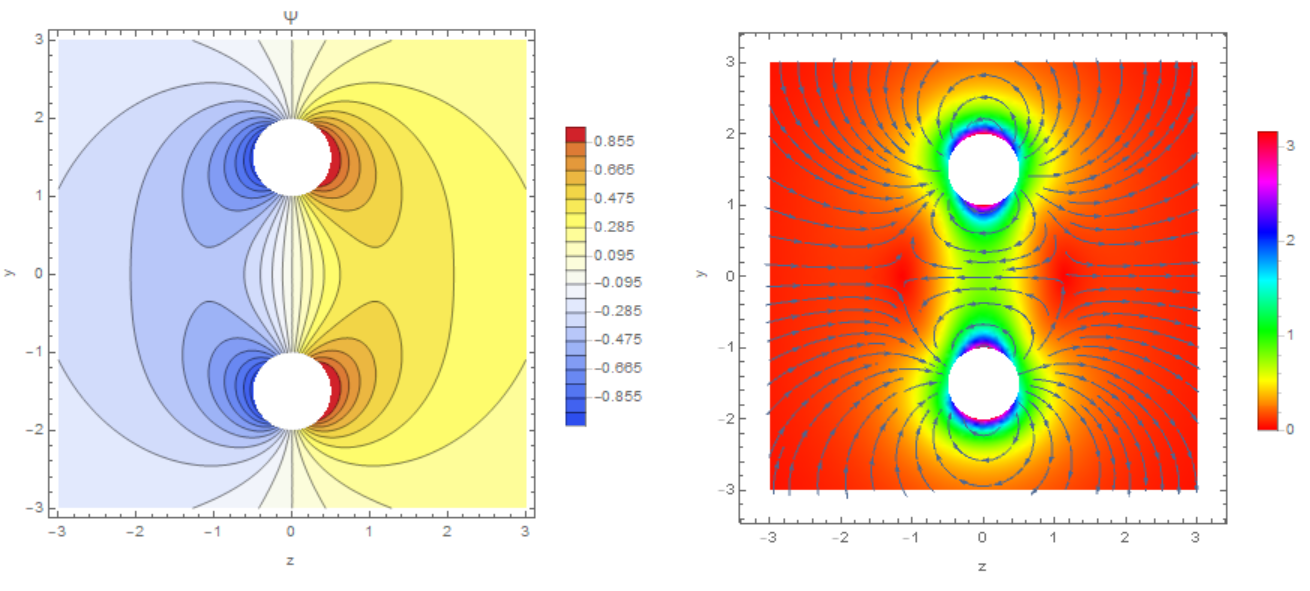
For a static case with constant magnetization, we use the scalar potential, for example
L1 = 5; L2 = 5; R1 = 1.5; L3 = 3;
Subscript[\[ScriptCapitalR], 1] =
ImplicitRegion[x^2 + (y - R1)^2 < .25, {x, y}];
Subscript[\[ScriptCapitalR], 2] =
ImplicitRegion[x^2 + (y + R1)^2 < .25, {x, y}];;
Subscript[\[ScriptCapitalR], 3] =
RegionUnion[Subscript[\[ScriptCapitalR], 1],
Subscript[\[ScriptCapitalR], 2]];
Subscript[\[ScriptCapitalR], 4] =
ImplicitRegion[-L1 <= x <= L1 && -L2 <= y <= L2, {x,
y}]; Subscript[\[ScriptCapitalR], 5] =
ImplicitRegion[-L3 <= x <= L3 && -L3 <= y <= L3, {x,
y}]; \[ScriptCapitalR]p =
RegionDifference[Subscript[\[ScriptCapitalR], 5],
Subscript[\[ScriptCapitalR], 3]];
\[ScriptCapitalR] =
RegionDifference[Subscript[\[ScriptCapitalR], 4],
Subscript[\[ScriptCapitalR], 3]];
RegionPlot[\[ScriptCapitalR]]
Us = NDSolveValue[{y*\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == -D[
u[x, y], y],
DirichletCondition[u[x, y] == Sin[Pi*x], x^2 + (y - R1)^2 == .25],
DirichletCondition[u[x, y] == Sin[Pi*x], x^2 + (y + R1)^2 == .25]},
u, {x, y} \[Element] \[ScriptCapitalR],
Method -> {"FiniteElement",
"MeshOptions" -> {"MaxCellMeasure" -> 0.0005}}]
H = -{D[Us[x, y], x], D[Us[x, y], y]};
{ContourPlot[Us[x, y], {x, y} \[Element] \[ScriptCapitalR]p,
Contours -> 20, FrameLabel -> {"z", "y"}, PlotRange -> All,
PlotLabel -> "\[CapitalPsi]", PlotLegends -> Automatic,
ColorFunction -> "TemperatureMap", PlotPoints -> 50], StreamDensityPlot[H, {x, y} \[Element] \[ScriptCapitalR]p,
PlotRange -> All, FrameLabel -> {"z", "y"},
AspectRatio -> Automatic, StreamPoints -> Automatic,
StreamScale -> Automatic, ColorFunction -> Hue,
PlotLegends -> Automatic]}