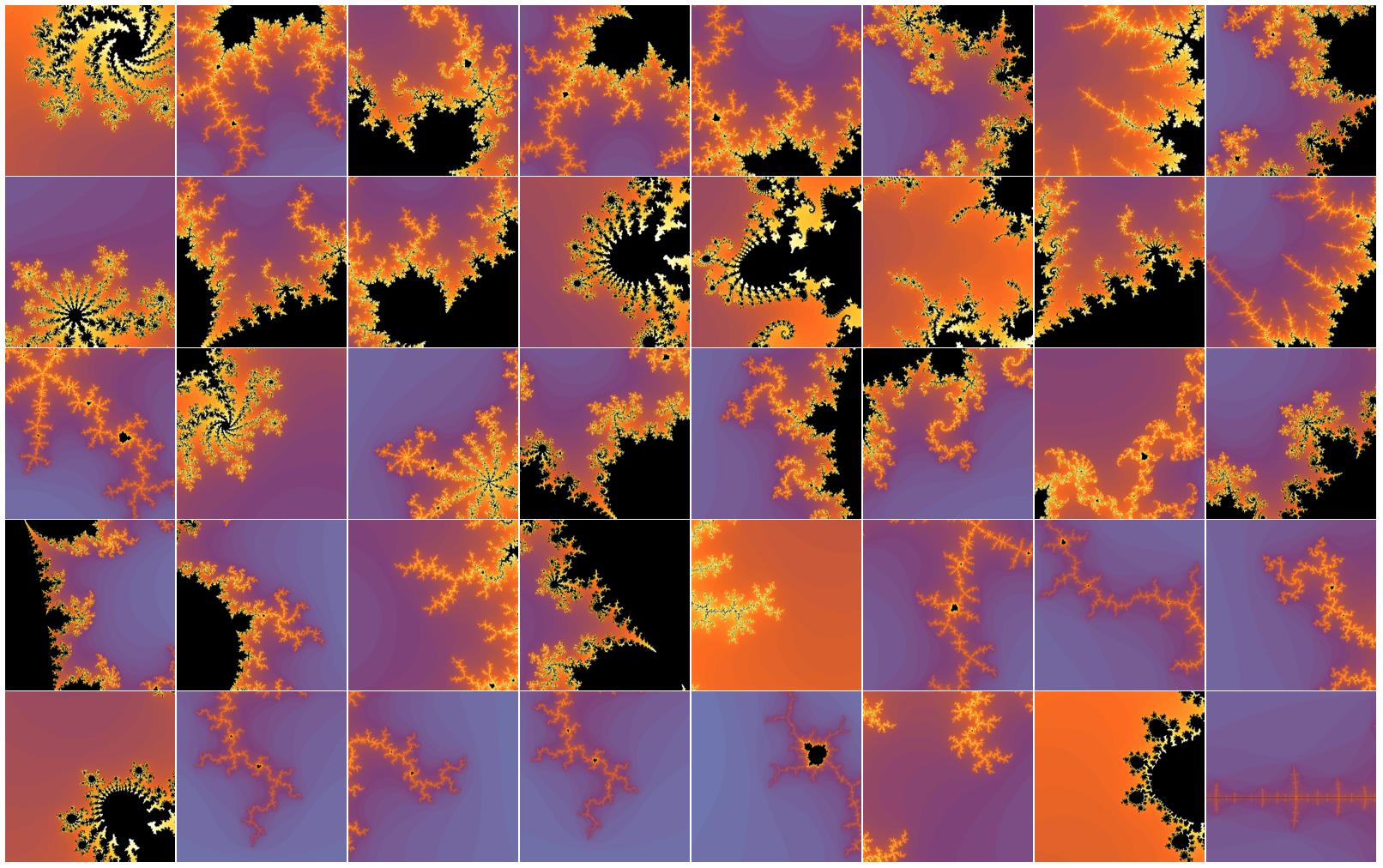
Mandelbrot fractal is an infinite universe where in many corners you can find beautiful structures. But some places are more stunning than the others, and some can be pretty dull still. Is there a way to automate finding "interesting" beautiful Mandelbrot structures? A method below uses a mix of complexity science, image processing and computational geometry to approach this problem. I start with final result where random Mandelbrot fractal samples are sorted form left to right and bottom to top in the order of decreasing image entropy. And indeed it is obvious to the naked eye that sophistication and beauty of structures drops too. If you or your colleagues are interested in immersion in such projects, apply for Wolfram Summer School. Read full article below the image.
NOTE: Click on image to zoom in. Then press browser's back button to return to reading the post.
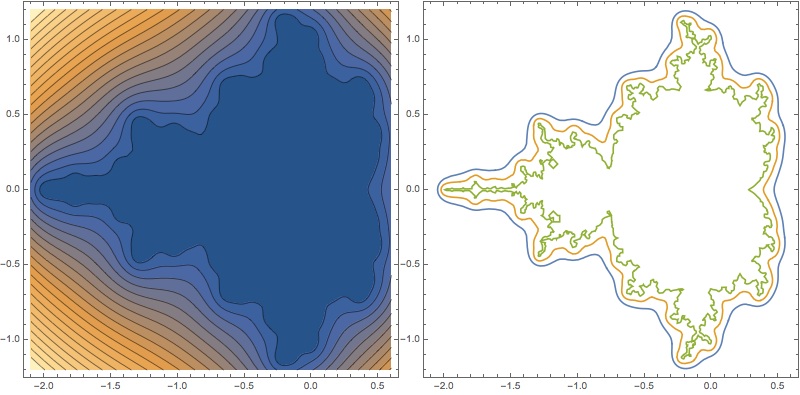
1. Define a function that approximates Mandelbrot set boundary
MandelbrotSetDistance can be used to approximates Mandelbrot set boundary with a smooth curve:
Row@{ContourPlot[Evaluate[MandelbrotSetDistance[x+I*y]],
{x,-2.1,.6},{y,-1.2,1.2},MaxRecursion->2,Contours->20,ImageSize->400],
ContourPlot[Evaluate[MandelbrotSetDistance[x+I*y]==#&/@{.2,.1,.01}],
{x,-2.1,.6},{y,-1.2,1.2},MaxRecursion->2,ImageSize->400]}
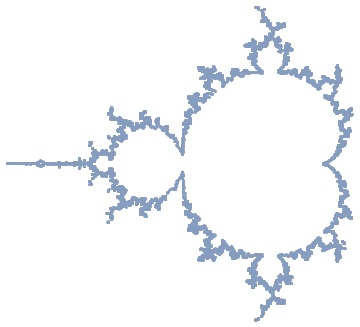
2. Define boundary approximation as a geometric region
We can now define boundary as a geometric region and we need to do this at high resolution to be really close to the most interesting regions. HINT: Play with MaxRecursion and proximity prox parameter
prox=.001;
reg=DiscretizeGraphics[ContourPlot[MandelbrotSetDistance[x+I*y]==prox,
{x,-2.1,.6},{y,-1.2,1.2},MaxRecursion->3]]
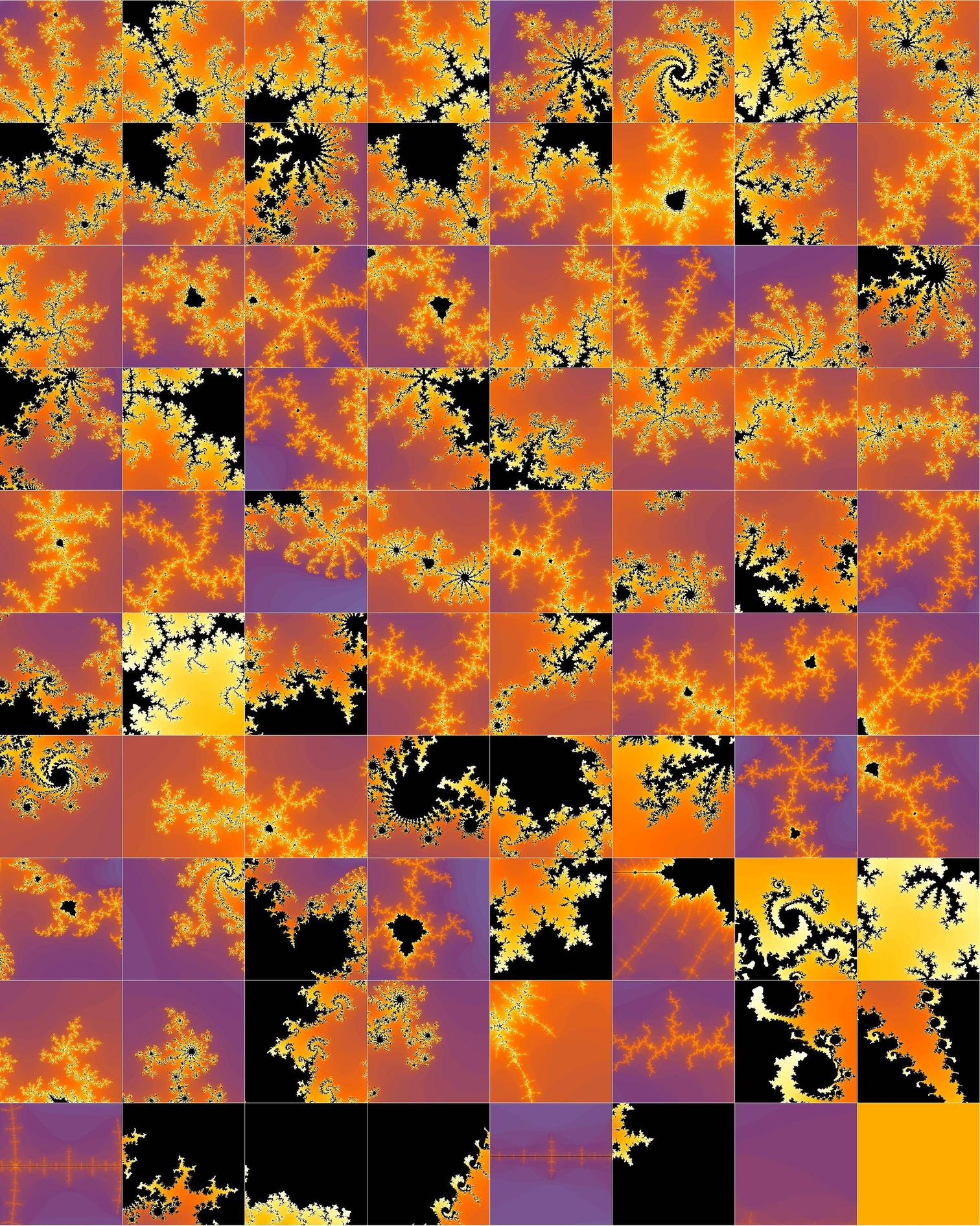
3. Use RandomPoint to sample fractal frames along boundary
See how sampling works for 1000 random points along the MS boundary:
Graphics[{PointSize[.001], Point[RandomPoint[reg, 10000]]}]
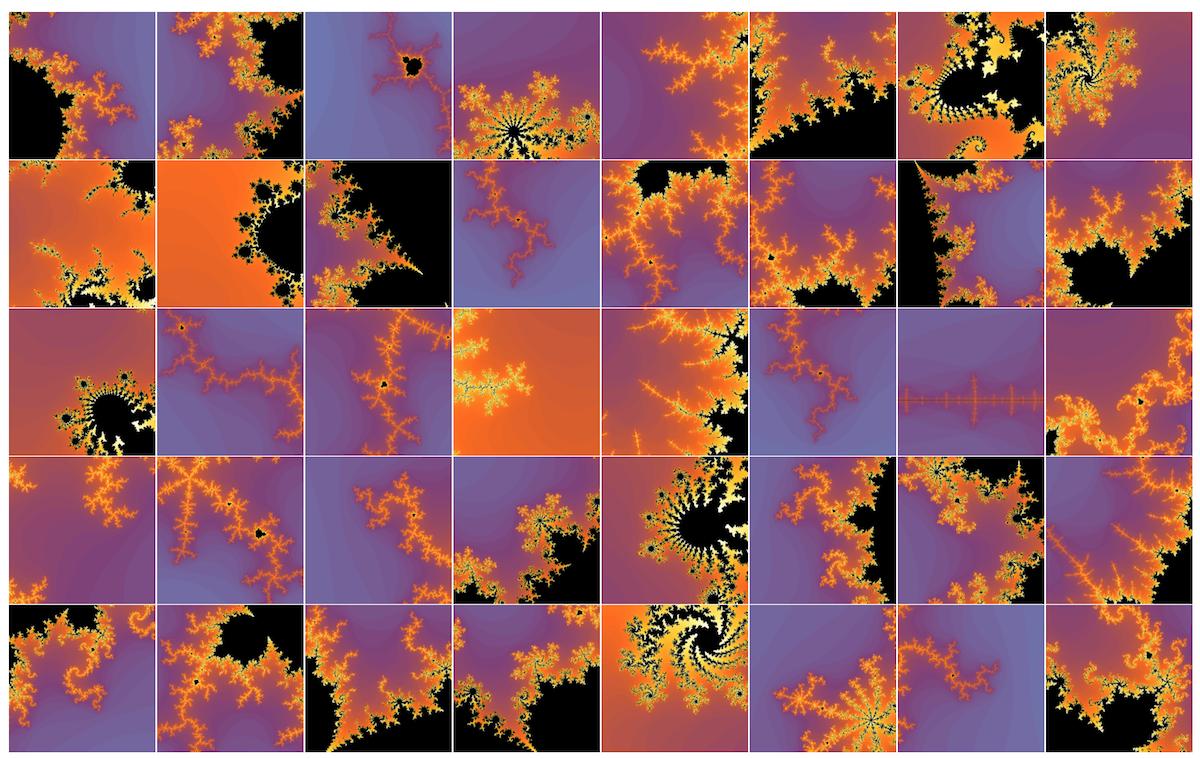
Define a function that puts a square of a random size smaller than 2d at a random point p in complex plane:
delta[d_][p_]:=With[{del={1,1}RandomReal[d]},{1,I}.#&/@{p-del,p+del}]
Now sample fractals of random zoom along the boundary. HINT: smaller d's in delta[d][p] give higher zoom frames.
pics=MandelbrotSetPlot[#,Frame->False,PlotRangePadding->None,
ImageSize->Tiny]&/@delta[.05]/@RandomPoint[reg,40];
Grid[Partition[pics,8],Spacings->{0, 0}]
4. Use image entropy as complexity measure to find the "interesting"
ImageMeasurements[image, "Entropy"] can help assess complexity of an image. Quoting lecture notes "image entropy is a quantity which is used to describe the `business' of an image, i.e. the amount of information which must be coded for by a compression algorithm. Low entropy images, such as those containing a lot of black sky, have very little contrast and large runs of pixels with the same or similar values. An image that is perfectly flat will have an entropy of zero. Consequently, they can be compressed to a relatively small size. On the other hand, high entropy images such as an image of heavily cratered areas on the moon have a great deal of contrast from one pixel to the next and consequently cannot be compressed as much as low entropy images."
Images need to be pre-processed before measuring entropy - especially to better identify almost-uniform backgrounds. GradientFilter is a useful derivative that flattens such backgrounds.
GradientFilter[ColorConvert[pics[[1]],"Grayscale"],1]//ImageAdjust

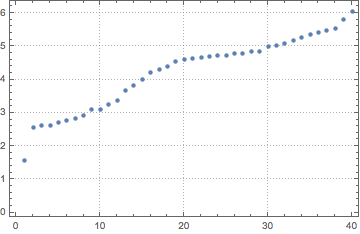
Verify that images do have different entropy:
measE[i_]:=ImageMeasurements[GradientFilter[
ColorConvert[i,"Grayscale"],1],"Entropy"]
ListPlot[Sort[measE/@pics],PlotTheme->"Detailed"]
Now we can reverse-sort by entropy and it is even obvious to the naked eye that first fractals are more "interesting". You can use this sorting to select just the first few as "interesting" and then for more complex images just repeat or increases the sample size.
sort=Reverse@SortBy[pics,measE];
Grid[Partition[sort,8],Spacings->{0, 0}]