(1) Why not use gradient within MATLAB?
(2) D[expr, t] is for symbolic derivatives, not numerical ones. You cannot use it to differentiate data, unless you construct a symbolic expression that depends on some variable(s) (e.g. t, etc.), such as Interpolation[data][t]. So I think there's something you have to figure out.
(3) Since you're new to Mathematica, here's an example:
Suppose you've manage to import your data into Mathematica. For the sake of an example, here's some Mathematica code to generate data that approximates the function
$\sin t$.
t = Subdivide[0., 2 Pi, 100]; (* Subdivide[] ~ linspace() in MATLAB *)
data = Sin[t];
One can plot data with ListLinePlot[data] (like plot(data)) or ListLinePlot[Transpose@{t, data}] (like plot(t, data)). The prefix notation func@arg, which is the same as func[arg], can be used on single-argument functions to reduce the number of nested brackets []. Whether this makes code easier to work with is a matter of taste and habits.
Mathematica has a function to differentiate this sort of data, but it's somewhat hidden inside the numerical differentiation contexts. It is called NDSolve`FiniteDifferenceDerivative and may be found in this tutorial.
grad = NDSolve`FiniteDifferenceDerivative[Derivative[1], t, data];
ListLinePlot[Transpose@{t, grad}]
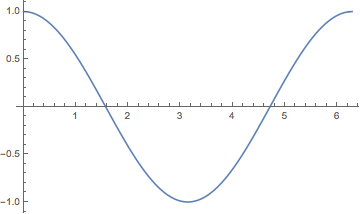
By default NDSolve`FiniteDifferenceDerivative will compute a 4th-order, finite-difference approximation to the derivative. This can be controlled by the option "DifferenceOrder":
grad = NDSolve`FiniteDifferenceDerivative[Derivative[1], t, data, "DifferenceOrder" -> 2];
This will yield nearly the same result as MATLAB's gradient (specifying appropriate spacing). The only difference is that at the endpoints of data, MATLAB uses an order-1 difference (i.e., the slopes between the first two points and the last two points) and Mathematica uses an order-2 formula.
You can also substitute Derivative[2] for Derivative[1] to approximate the second derivative, and so forth. As you may know, the higher the derivative, the more the noise is amplified.
As Gustavo has said, you can use MATLink to do all the necessary communication between Mathematic and MATLink for this.