Hi Bernat, I was looking into the examples yesterday, but wanted something more along the lines of the standard ant colony optimization
http://en.wikipedia.org/wiki/Ant_colony_optimization_algorithms
So I started playing with the concepts, just trying ants walking randomnly without update on the pherormone field. Just setting up n number of ants and letting them walk.
Using the model of the confetti found here
http://mathematica.stackexchange.com/questions/1900/how-can-this-confetti-code-be-improved-to-include-shadows-and-gravity/2296#2296I came up with the following piece of code.
ymax = 1000; xmax = 1000;
nest = {500, 500};
maxAnts = 30;
steps = 200;
maxSpeed = 20;
maxAngle = \[Pi]/6;
orientation =
RandomVariate[UniformDistribution[{0, 2 \[Pi]}], maxAnts];
ant = Table[
agent[\[Infinity], nest, orientation[[i]], #] & /@ Range[i], {i,
maxAnts}];
update[agent[symbol_, location_, direction_, t_]] :=
Module[{dir, speed, loc},
dir = First@
RandomVariate[
UniformDistribution[{direction - maxAngle,
direction + maxAngle}], 1];
speed = RandomVariate[UniformDistribution[{1, maxSpeed}], 1];
loc = Flatten[location + Round[{speed*Cos[dir], speed*Sin[dir]}]];
loc = Min[#] & /@ Transpose[{loc, {xmax, ymax}}];
loc = Max[#] & /@ Transpose[{loc, {0, 0}}];
agent[symbol, loc, dir, t + 1]]
display[agent[symbol_, location_, direction_, t_]] :=
Text[Rotate[symbol, direction], location]
display[list_] := Module[{lst = display[#] & /@ list}, Graphics[lst]]
history =
Join[ant[[#]],
NestList[update, Last@ant[[#]], steps - Length[ant[[#]]]]] & /@
Range[maxAnts];
Animate[Show[Graphics[display[history[[All, i]]]],
Graphics[{Red, PointSize[Large], Point[nest]}],
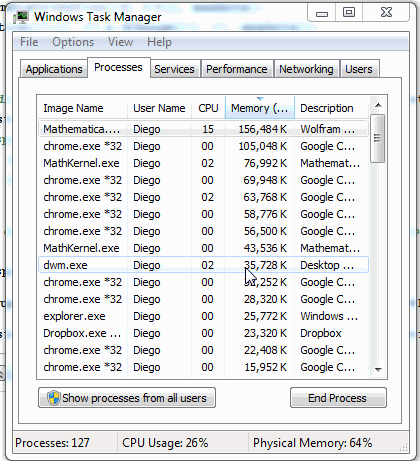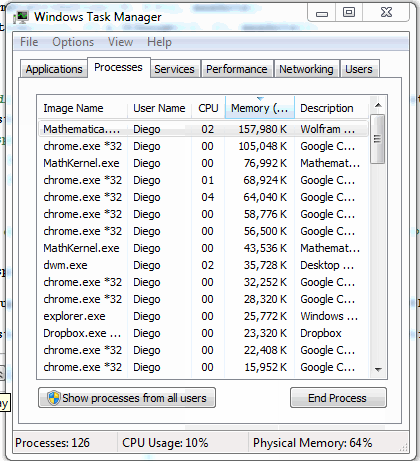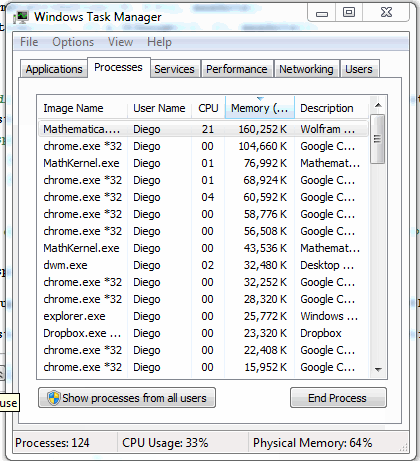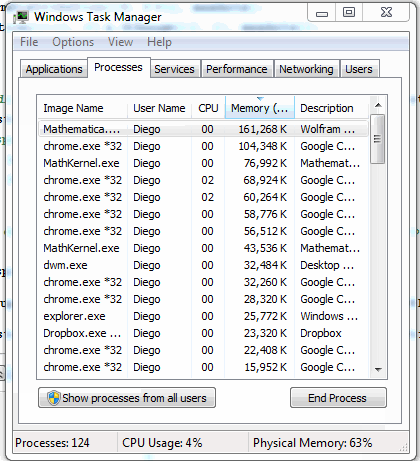
PlotRange -> {{0, xmax}, {0, ymax}}], {i, 1, steps, 1}]
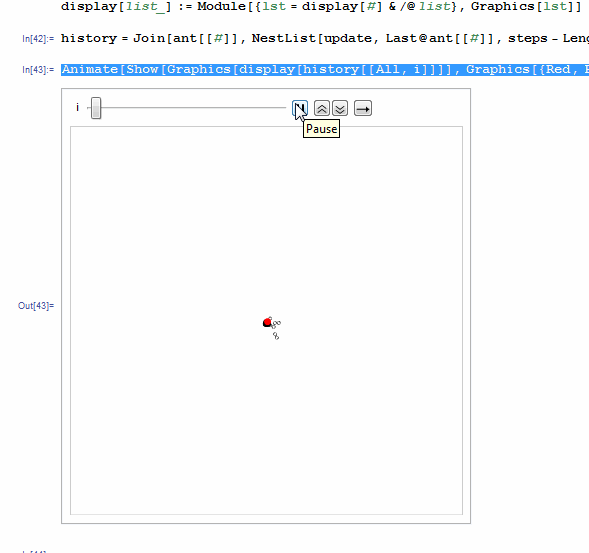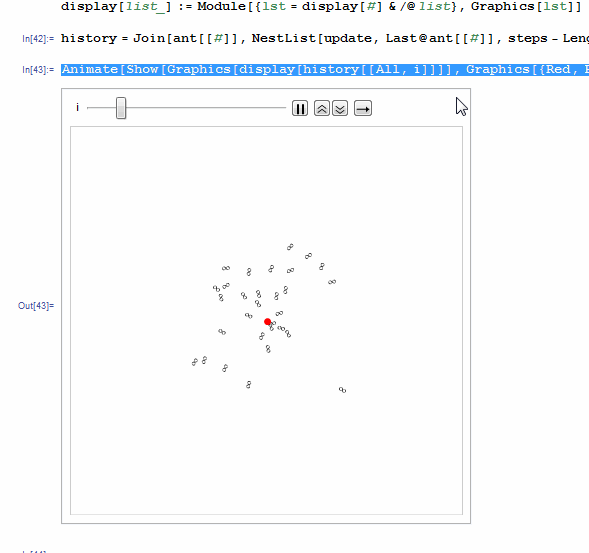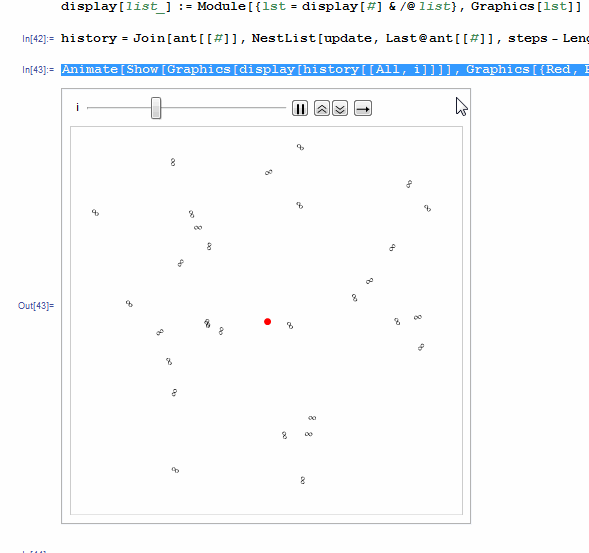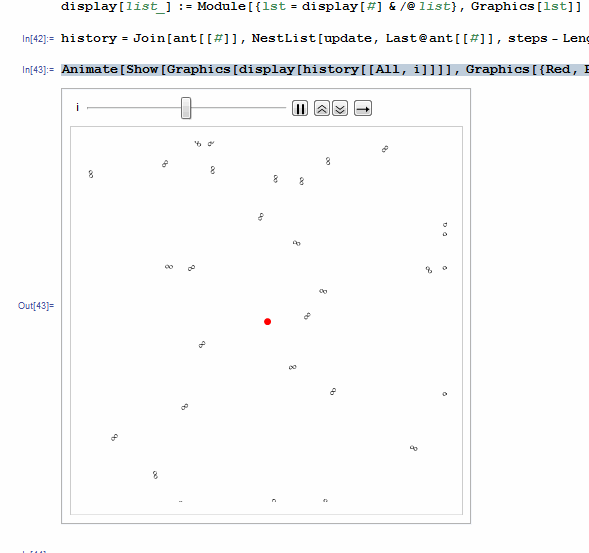
The issue I have is that Mathematica seems to have a memory leak, as the Animate, or manipulate, or exporting to gif runs, the amount of memory allocated to Mathematica keeps growing until it just stops working. Below is a gif in which I turn the animation on and off to show that the memory keeps growing as Animate (or Manipulate) runs. A bummer because this limits the number of ants and steps to use. Hope we can get some feedback on what is going on.