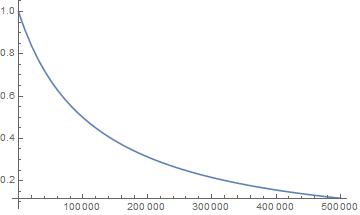
The code below gives incorrect 2nd derivative. figure 1 shows the original function xxSumS1[s, r] = funDervtveLAB[s, r, 0] when r=200, while second figure shows the 1st derivative of the original function "Exp[-noisepows]laplaceLABs[s, r]" when r=200. The 1st derivative is correct as the 1st derivative of a decreasing function is negative (figure 2). However, the 2nd derivative "xxSumS3[s, r] = funDervtveLAB[s, r, 2] when r=200" seems to be incorrect. This is because I expect it to be positive for all values of s as it is the derivative of the 1st derivative and the 1st derivative is an increasing function in s. Figure 3 shows the 2nd derivative of the original function


Clear["Global`*"]
a = 4.88; b = 0.43; etaLAB = 10.^(-0.1/10); etaNAB = 10.^(-21/10); etaTB = etaNAB;
PtABdB = 32; PtAB = 10^(PtABdB/10)*1*^-3; PtTBdB = 40; PtTB = 10^(PtTBdB/10)*1*^-3;
NF = 8; BW = 1*^7; noisepowdBm = -147 - 30 + 10*Log[10, BW] + NF;
noisepow = 0; RmaxLAB = 20000;
TBdensity = 1*^-6; ABdensity = 1*^-6;
alfaLAB = 2.09; alfaNAB = 2.09; alfaTB = 2.09;
mparameter = 3;
zetaLAB = PtAB*etaLAB; zetaNAB = PtAB*etaNAB; zetaTB = PtTB*etaTB;
height = 100; sinrdBrange = -10; sinr = 10.^(sinrdBrange/10);
probLoSz[z_] := 1/(1 + a*Exp[-b*(180/Pi*N[ArcTan[height/z]] - a)]);
probLoSr[r_] := 1/(1 + a*Exp[-b*(180/Pi*N[ArcTan[height/Sqrt[r^2 - height^2]]] -
a)]);
funLoS[z_] := z*probLoSz[z];
funNLoS[z_] := z*(1 - probLoSz[z]);
funLABNABs[z_, s_] := (1 - 1/(1 + s*zetaNAB*(z^2 + height^2)^(-alfaNAB/2)))*funNLoS[z];
funLABLABs[z_,
s_] := (1 - (mparameter/(mparameter + s*zetaLAB*(z^2 + height^2)^(-alfaLAB/2)))^mparameter)*funLoS[z];
funLABTBs[z_, s_] := z*(1 - 1/(1 + s*zetaTB*z^(-alfaTB)));
distnceLABNABs = (zetaLAB/zetaNAB)^(1/alfaLAB)*height^(alfaNAB/alfaLAB);
NearstInterfcLABNABs[r_] := Piecewise[{{height, r <= distnceLABNABs}, {(zetaNAB/zetaLAB)^(1/alfaNAB)* r^(alfaLAB/alfaNAB), r > distnceLABNABs}}];
NearstInterfcLABTBs[r_] := (zetaTB/zetaLAB)^(1/alfaTB)*r^(alfaLAB/alfaTB);
NearstInterfcLABLABs[r_] := r;
lowerlimitLABNABs[r_] := Sqrt[NearstInterfcLABNABs[r]^2 - height^2];
lowerlimitLABLABs[r_] := Sqrt[NearstInterfcLABLABs[r]^2 - height^2];
lowerlimitLABTBs[r_] := NearstInterfcLABTBs[r];
InteglaplaceLABNABs[s_?NumericQ, r_?NumericQ] := NIntegrate[funLABNABs[z, s], {z, lowerlimitLABNABs[r], RmaxLAB}];
InteglaplaceLABLABs[s_?NumericQ, r_?NumericQ] := NIntegrate[funLABLABs[z, s], {z, lowerlimitLABLABs[r], RmaxLAB}];
InteglaplaceLABTBs[s_?NumericQ, r_?NumericQ] := NIntegrate[funLABTBs[z, s], {z, lowerlimitLABTBs[r], RmaxLAB}];
laplaceLABNABs[s_, r_] := Exp[-2*Pi*ABdensity*InteglaplaceLABNABs[s, r]];
laplaceLABLABs[s_, r_] := Exp[-2*Pi*ABdensity*InteglaplaceLABLABs[s, r]];
laplaceLABTBs[s_, r_] := Exp[-2*Pi*TBdensity*InteglaplaceLABTBs[s, r]];
laplaceLABs[s_, r_] :=
laplaceLABNABs[s, r]*laplaceLABLABs[s, r]*laplaceLABTBs[s, r];
funDervtveLAB[s_, r_, kk_] := D[Exp[-noisepow*s]*laplaceLABs[s, r], {s, kk}];
xxSumS1[s_, r_] = funDervtveLAB[s, r, 0]; (*original function*)
xxSumS2[s_, r_] = funDervtveLAB[s, r, 1]; (* 1st derivative*)
xxSumS3[s_, r_] = funDervtveLAB[s, r, 2]; (*2nd derivative*)
xxSumR1[r_] := xxSumS1[s, r] /. s -> (mparameter*sinr/zetaLAB*r^alfaLAB);
xxSumR2[r_] := xxSumS2[s, r] /. s -> (mparameter*sinr/zetaLAB*r^alfaLAB);
xxSumR3[r_] := xxSumS3[s, r] /. s -> (mparameter*sinr/zetaLAB*r^alfaLAB);