Two months ago, Albert Rich posted "What's the hardest integral Mathematica running Rubi can find?" here on the Wolfram Community. You might have also seen that I responded in detail, and pointed out a few things that could help improve Rubi (Rule-based integrator). While it appears nothing really happened afterward, this is far from reality. Since then, Albert and I have worked closely together to make Rubi more accessible and user-friendly. If you would like to learn how our productive collaboration evolved, let me invite you to read my latest blog-post. However, here, we want to share an update that should serve as an overview of what we have done to improve Rubi.

First of all, Rubi has got a new home under rulebasedintegration.org, and its old website will no longer be updated. On the new website, you will find information, installation instructions, and links to the source-code and test-suites.

Secondly, we created a Rubi Organization on GitHub that serves as the headquarters for all things Rubi. It contains all Rubi's code, notebooks, and test-suites nicely structured into several repositories. At the moment, we provide repositories for the

• loadable package files and notebook source files defining over 6700 integration rules,
• PDF files displaying the rules in human-readable mathematical notation alongside the Mathematica code, and
• test-suite files containing over 71000 integration problems and their solutions.

The integration test files are available in the syntax used by 4 popular computer algebra systems (Mathematica, Maple, Maxima, and Axiom). The test-suite can be used to compare Rubi's results with other symbolic integrators, including Mathematica's Integrate function.

In addition to the transition to GitHub, we recently released version 4.16.0.3 of Rubi which significantly expands the class of expressions the system can integrate. But the most noticeable change for users is the completely reworked display of the rules and intermediate steps Rubi uses to integrate expressions. Although installation, usage, and examples are given on Rubi's website, let me show you how easy it is to install and run Rubi 4.16.0.3 using Mathematica 11.3:

The command

PacletInstall["https://github.com/RuleBasedIntegration/Rubi/releases/download/4.16.0.3/Rubi-4.16.0.3.paclet"];

installs the Rubi-4.16.0.3 paclet on your computer. After that, to load Rubi into Mathematica all you have to do is issue the Get command

<< Rubi`

Then to integrate an expression with respect to a variable, use Rubi's Int command similar to Mathematica's Integrate command. For example, evaluating

Int[(Sec[x]^2 + Sec[x]^2*Tan[x])/((2 - Tan[x])*Sqrt[1 + Tan[x]^3]), x]

returns the antiderivative (a.k.a. the indefinite integral)

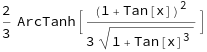
Rubi's unique ability to display the steps it uses to integrate expressions is a great feature of the system. For example, the Steps command

Steps@Int[(Sec[x]^2 + Sec[x]^2*Tan[x])/((2 - Tan[x])*Sqrt[1 + Tan[x]^3]), x]

displays

Here, in red are the rules used to integrate the expression, and in blue are the intermediate results. Each rule can be expanded to show the rule number, which directly corresponds to the index of the rule in Int's list of DownValues. More importantly, you can see the conditions that have to be satisfied so the rule can be applied.

Rubi's Stats command provides statistics about the integration. For example,

Stats[Int[(Sec[x]^2 + Sec[x]^2*Tan[x])/((2 - Tan[x])*Sqrt[1 + Tan[x]^3]), x]]

displays

The leaf-count size of an antiderivative is a crude measure of its complexity. As you can see, Rubi's antiderivative for this integral has a leaf-count of 25. Now compare Rubi's antiderivative with that produced by Mathematica 11.3 for the same integral:

Integrate[(Sec[x]^2 + Sec[x]^2*Tan[x])/((2 - Tan[x])*Sqrt[1 + Tan[x]^3]), x]

LeafCount[%]
(*  290 *)

Note that not only is Mathematica's result more than 11 times the size of Rubi's, it unnecessarily involves elliptic integral functions and the imaginary unit.

Skeptics might be inclined to ask if Rubi's dramatically simpler result is actually a valid antiderivative. Since symbolic differentiation is much easier than integration, antiderivatives can be verified correct by seeing if its derivative equals the original integrand as follows:

expr = (Sec[x]^2 + Sec[x]^2*Tan[x])/((2 - Tan[x])*Sqrt[1 + Tan[x]^3]);
FullSimplify[D[Int[expr, x], x] == expr]
FullSimplify[D[Integrate[expr, x], x] == expr]

As you can see Mathematica easily verifies Rubi's antiderivative correct, but has a hard time verifying its own antiderivative correct...

Albert and I are working on publishing the program used to thoroughly test each new version of Rubi before being released. The test program ensures Rubi's result equals the optimal antiderivative for the over 71000 problems in the test-suite. And yes, the optimal antiderivatives have all been verified correct by differentiation.

Of course, the optimal antiderivatives stored in the test-suite are actually just the simplest ones found so far. If you should find a substantially simpler antiderivative than the one in the test-suite, please report it so the test-suite can be made even harder on Rubi!

If all that has got you interested in joining Rubi's community of users, check out its website or talk to us in our Gitter chatroom.