I generate a music with reference to MidiNet. Most neural network models for music generation use recurrent neural networks. However, MidiNet use convolutional neural networks. There are three models in MidiNet. Model 1 is Melody generator, no chord condition. Model 2,3 are Melody generators with chord condition. I try Model 1, because it is most interesting in the three models compared in the paper.
Get MIDI data
My favorite Jazz bassist is Jaco Pastorius. I get MIDI data from here. For example, I get MIDI data of "The Chicken".
url = "http://www.midiworld.com/download/1366";
notes = Select[Import[url, {"SoundNotes"}], Length[#] > 0 &];
There are some styles in the notes. I get base style from them.
notes[[All, 3, 3]]
Sound[notes[[1]]]
I change MIDI data to Image data. I fix the smallest note unit to be the sixteenth note. I divide the MIDI data into the sixteenth note period and select the sound found at the beginning of each period. And the pitch of SoundNote function is from 1 to 128. So, I change one bar to grayscale image(h=128*w=16). First, I create the rule to change each note pitch(C-1,...,G9) to number(1,...,128), C4 -> 61.
codebase = {"C", "C#", "D", "D#", "E" , "F", "F#", "G", "G#" , "A",
"A#", "B"};
num = ToString /@ Range[-1, 9];
pitch2numberrule =
Take[Thread[
StringJoin /@ Reverse /@ Tuples[{num, codebase}] ->
Range[0, 131] + 1], 128]

Next, I change each bar to image (h = 128*w = 16).
tempo = 108;
note16 = 60/(4*tempo); (* length(second) of 1the sixteenth note *)
select16[snlist_, t_] :=
Select[snlist, (t <= #[[2, 1]] <= t + note16) || (t <= #[[2, 2]] <=
t + note16) || (#[[2, 1]] < t && #[[2, 2]] > t + note16) &, 1]
selectbar[snlist_, str_] :=
select16[snlist, #] & /@ Most@Range[str, str + note16*16, note16]
selectpitch[x_] := If[x === {}, 0, x[[1, 1]]] /. pitch2numberrule
pixelbar[snlist_, t_] := Module[{bar, x, y},
bar = selectbar[snlist, t];
x = selectpitch /@ bar;
y = Range[16];
Transpose[{x, y}]
]
imagebar[snlist_, t_] := Module[{image},
image = ConstantArray[0, {128, 16}];
Quiet[(image[[129 - #[[1]], #[[2]]]] = 1) & /@ pixelbar[snlist, t]];
Image[image]
]
soundnote2image[soundnotelist_] := Module[{min, max, data2},
{min, max} = MinMax[#[[2]] & /@ soundnotelist // Flatten];
data2 = {#[[1]], #[[2]] - min} & /@ soundnotelist;
Table[imagebar[data2, t], {t, 0, max - min, note16*16}]
]
(images1 = soundnote2image[notes[[1]]])[[;; 16]]

Create the training data
First, I drop images1 to an integer multiple of the batch size. Its length is 128 bars and about 284 seconds with a batch size of 16.
batchsize = 16;
getbatchsizeimages[i_] := i[[;; batchsize*Floor[Length[i]/batchsize]]]
imagesall = Flatten[Join[getbatchsizeimages /@ {images1}]];
{Length[imagesall], Length[imagesall]*note16*16 // N}
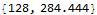
MidiNet proposes a novel conditional mechanism to use music from the previous bar to condition the generation of the present bar to take into account the temporal dependencies across a different bar. So, each training data of MidiNet (Model 1: Melody generator, no chord condition) consists of three "noise", "prev", "Input". "noise" is a 100-dimensions random vector. "prev" is an image data(112816) of the previous bar. "Input" is an image data(112816) of the present bar. The first "prev" of each batch is all 0. I generate training data with a batch size of 16 as follows.
randomDim = 100;
n = Floor[Length@imagesall/batchsize];
noise = Table[RandomReal[NormalDistribution[0, 1], {randomDim}],
batchsize*n];
input = ArrayReshape[ImageData[#], {1, 128, 16}] & /@
imagesall[[;; batchsize*n]];
prev = Flatten[
Join[Table[{{ConstantArray[0, {1, 128, 16}]},
input[[batchsize*(i - 1) + 1 ;; batchsize*i - 1]]}, {i, 1, n}]],
2];
trainingData =
AssociationThread[{"noise", "prev",
"Input"} -> {#[[1]], #[[2]], #[[3]]}] & /@
Transpose[{noise, prev, input}];
Create GAN
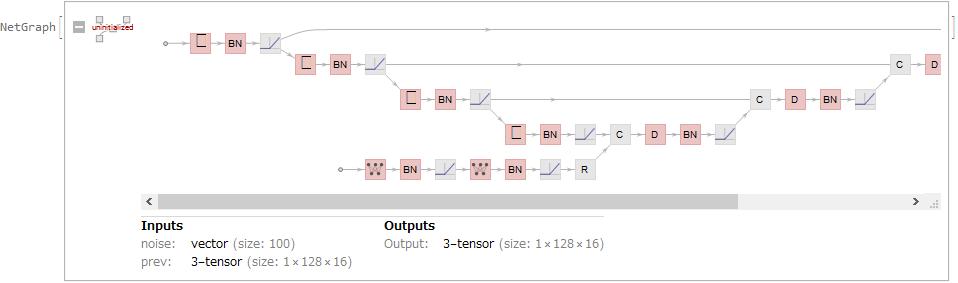
I create generator with reference to MidiNet.
generator = NetGraph[{
1024, BatchNormalizationLayer[], Ramp, 256,
BatchNormalizationLayer[], Ramp, ReshapeLayer[{128, 1, 2}],
DeconvolutionLayer[64, {1, 2}, "Stride" -> {2, 2}],
BatchNormalizationLayer[], Ramp,
DeconvolutionLayer[64, {1, 2}, "Stride" -> {2, 2}],
BatchNormalizationLayer[], Ramp,
DeconvolutionLayer[64, {1, 2}, "Stride" -> {2, 2}],
BatchNormalizationLayer[], Ramp,
DeconvolutionLayer[1, {128, 1}, "Stride" -> {2, 1}],
LogisticSigmoid,
ConvolutionLayer[16, {128, 1}, "Stride" -> {2, 1}],
BatchNormalizationLayer[], Ramp,
ConvolutionLayer[16, {1, 2}, "Stride" -> {1, 2}],
BatchNormalizationLayer[], Ramp,
ConvolutionLayer[16, {1, 2}, "Stride" -> {1, 2}],
BatchNormalizationLayer[], Ramp,
ConvolutionLayer[16, {1, 2}, "Stride" -> {1, 2}],
BatchNormalizationLayer[], Ramp, CatenateLayer[],
CatenateLayer[], CatenateLayer[],
CatenateLayer[]}, {NetPort["noise"] ->
1, NetPort["prev"] -> 19,
19 -> 20 ->
21 -> 22 -> 23 -> 24 -> 25 -> 26 -> 27 -> 28 -> 29 -> 30,
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7, {7, 30} -> 31,
31 -> 8 -> 9 -> 10, {10, 27} -> 32,
32 -> 11 -> 12 -> 13, {13, 24} -> 33,
33 -> 14 -> 15 -> 16, {16, 21} -> 34, 34 -> 17 -> 18},
"noise" -> {100}, "prev" -> {1, 128, 16}
]
I create discriminator which does not have BatchNormalizationLayer and LogisticSigmoid, because I use Wasserstein GAN easy to stabilize the training.
discriminator = NetGraph[{
ConvolutionLayer[64, {89, 4}, "Stride" -> {1, 1}], Ramp,
ConvolutionLayer[64, {1, 4}, "Stride" -> {1, 1}], Ramp,
ConvolutionLayer[16, {1, 4}, "Stride" -> {1, 1}], Ramp,
1},
{1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7}, "Input" -> {1, 128, 16}
]

I create Wasserstein GAN network.
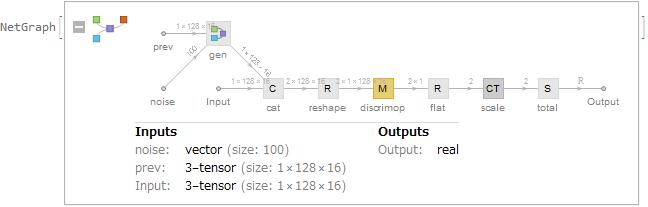
ganNet = NetInitialize[NetGraph[<|"gen" -> generator,
"discrimop" -> NetMapOperator[discriminator],
"cat" -> CatenateLayer[],
"reshape" -> ReshapeLayer[{2, 1, 128, 16}],
"flat" -> ReshapeLayer[{2}],
"scale" -> ConstantTimesLayer["Scaling" -> {-1, 1}],
"total" -> SummationLayer[]|>,
{{NetPort["noise"], NetPort["prev"]} -> "gen" -> "cat",
NetPort["Input"] -> "cat",
"cat" ->
"reshape" -> "discrimop" -> "flat" -> "scale" -> "total"},
"Input" -> {1, 128, 16}]]
NetTrain
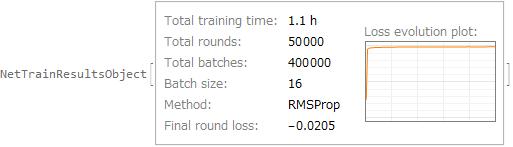
I train by using the training data created before. I use RMSProp as the method of NetTrain according to Wasserstein GAN. It take about one hour by using GPU.
net = NetTrain[ganNet, trainingData, All, LossFunction -> "Output",
Method -> {"RMSProp", "LearningRate" -> 0.00005,
"WeightClipping" -> {"discrimop" -> 0.01}},
LearningRateMultipliers -> {"scale" -> 0, "gen" -> -0.2},
TargetDevice -> "GPU", BatchSize -> batchsize,
MaxTrainingRounds -> 50000]
Create MIDI
I create image data of 16 bars by using generator of trained network.
bars = {};
newbar = Image[ConstantArray[0, {1, 128, 16}]];
For[i = 1, i < 17, i++,
noise1 = RandomReal[NormalDistribution[0, 1], {randomDim}];
prev1 = {ImageData[newbar]};
newbar =
NetDecoder[{"Image", "Grayscale"}][
NetExtract[net["TrainedNet"], "gen"][<|"noise" -> noise1,
"prev" -> prev1|>]];
AppendTo[bars, newbar]
]
bars

I select only the pixel having the max value among each column of the image, because there is a feature that the image generated by Wasserstein GAN is blurred. I clear the images.
clearbar[bar_, threshold_] := Module[{i, barx, col, max},
barx = ConstantArray[0, {128, 16}];
col = Transpose[bar // ImageData];
For[i = 1, i < 17, i++,
max = Max[col[[i]]];
If[max >= threshold,
barx[[First@Position[col[[i]], max, 1], i]] = 1]
];
Image[barx]
]
bars2 = clearbar[#, 0.1] & /@ bars

I change the image to SoundNote. I concatenate the same continuous pitches.
number2pitchrule = Reverse /@ pitch2numberrule;
images2soundnote[img_, start_] :=
SoundNote[(129 - #[[2]]) /.
number2pitchrule, {(#[[1]] - 1)*note16, #[[1]]*note16} + start,
"ElectricBass", SoundVolume -> 1] & /@
Sort@(Reverse /@ Position[(img // ImageData) /. (1 -> 1.), 1.])
snjoinrule = {x___, SoundNote[s_, {t_, u_}, v_, w_],
SoundNote[s_, {u_, z_}, v_, w_], y___} -> {x,
SoundNote[s, {t, z}, v, w], y};
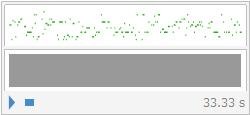
I generate music and attach its mp3 file.
Sound[Flatten@
MapIndexed[(images2soundnote[#1, note16*16*(First[#2] - 1)] //.
snjoinrule) &, bars2]]
Conclusion
I try music generation with GAN. I am not satisfied with the result. I think that the causes are various, poor training data, poor learning time, etc. Jaco is gone. I hope Neural Networks will be able to express Jaco's base.
 Attachments:
Attachments: