So let me start then. In the EPM textbook you can find Exercise 17 on page 342; chapter 8.4 covers the Examples section of chapter 8 which is all about Graphics and visualization. This exercise can be seen as the culmination of all previous treatments of triangles (see page 421, Index). It asks the student to program a dynamic triangle showing various triangle centers and the so-called Euler line, plus a color-coded legend. As of yet, there is no public/official solution given in the *.nb solutions manual. That's one more reason/motivation why it makes sense to share our solution suggestions to this particular exercise ;-)
Here we go, this is how i edited the ~50MB *.nb file at that location:
EPM1 Ch8.4 Exercise 17
17. (* Wellin solution to appear *) See Section 8.1 Exercise 11.
ClearAll[triangleCentroids]
We are opting for a Manipulate[Module[
]] idiom because it is the easiest transition from a static to a dynamic output when the problem or the output is simple and straight-forward on its own. Here the output is a single triangle in planar space, it cannot get any simpler than that! Note that under the hood Manipulate is composed of a DynamicModule[{init},Dynamic[
]] construct, which means that in reality our idiom is a DynamicModule[{init},Dynamic[Module[
]]] construct after all.
Options[triangleCentroids] = Options[Graphics];
triangleCentroids[{p1_, p2_, p3_}, opts : OptionsPattern[]] :=
Manipulate[
Module[
{
vertices, A, B, C, (*triangle vertex*)
rA, rB, rC, (*auxiliary vector in 3-D space*)
edges, edgecoords, (*triangle edge {edgea,edgeb,edgec}*)
midpts, (*midpoint of triangle edge {Ma,Mb,Mc}*)
medians, (*median line of triangle edge {meda,medb,medc}*)
centroid, (*centroid of triangle*)
circumcircle, circumcenter, (*circumsphere of triangle*)
circumradii, (*radius of circumsphere {cira,cirb,circ}*)
incircle, incenter, (*insphere of triangle*)
bisectrices, (*bisectrix at vertex {bisecA,bisecB,bisecC}*)
foots, (*interior/exterior foot on triangle edge {Fa,Fb,Fc}*)
altitudes, (*altitude on triangle edge {alta,altb,altc}*)
orthocenter, x, y, (*orthocenter of triangle*)
euler (*Euler line*)
},
{A, B, C} = {locA, locB, locC};
{rA, rB, rC} = {A, B, C} /. {x_, y_} :> {x, y, 0}; (*convert to 3-D coords*)
If[
Negative[Cross[rB - rA, rC - rA].{0, 0, 1}]
, {B, C} = {locC, locB} (*vertex naming convention counterclockwise*)
];
vertices = {A, B, C};
edgecoords = Reverse[Subsets[vertices, {2}]]; (*{{B,C},{A,C},{A,B}}*)
edges = Line /@ edgecoords; (*{edgea,edgeb,edgec}*)
midpts = RegionCentroid /@ edges; (*{Ma,Mb,Mc}*)
medians = MapThread[HalfLine[{#1, #2}] &, {vertices, midpts}]; (*{meda,medb,medc}*)
centroid = RegionCentroid[Triangle[vertices]];
circumcircle = Circumsphere[vertices];
circumcenter = RegionCentroid[circumcircle];
circumradii = Map[HalfLine[{circumcenter, #}] &, midpts]; (*{cira,cirb,circ}*)
incircle = Insphere[vertices];
incenter = RegionCentroid[incircle];
bisectrices = Map[HalfLine[{#, incenter}] &, vertices]; (*{bisecA,bisecB,bisecC}*)
foots = MapThread[RegionNearest[InfiniteLine[#1], #2] &, {edgecoords, vertices}]; (*{Fa,Fb,Fc}*)
altitudes = MapThread[InfiniteLine[{#1, #2}] &, {vertices, foots}] ; (*{alta,altb,altc}*)
orthocenter = RegionIntersection[altitudes[[1]], altitudes[[2]]];
euler = InfiniteLine[{centroid, circumcenter}];
Legended[
Graphics[
{
{EdgeForm[Gray], LightBlue, Triangle[vertices]}
, {PointSize[Medium], Red, Point[vertices]}
, Text[Style["A", 20, Bold], A]
, Text[Style["B", 20, Bold], B]
, Text[Style["C", 20, Bold], C]
, {PointSize[Medium], Green, Point[midpts]}
, {Opacity[.5], Green, Thickness[Small], medians}
, {PointSize[Large], Green, Point[centroid]}
, {Gray, circumcircle}
, {Opacity[.5], Gray, Thickness[Small], circumradii}
, {PointSize[Large], Gray, Point[circumcenter]}
, {Pink, incircle}
, {Opacity[.5], Red, Thickness[Small], bisectrices}
, {PointSize[Large], Pink, Point[incenter]}
, {PointSize[Medium], Blue, Point[foots]}
, {Opacity[.25], Blue, Thickness[Small], altitudes}
, {PointSize[Large], Blue, orthocenter}
, {Orange, Dashed, euler}
}
, opts
, PlotLabel -> Style[Framed["triangle centers"], 26, Blue, Background -> Lighter[Yellow]]
], Placed[
TableForm[{
{Style["A", Bold, Black], Style[ToString@A, Red]}
, {Style["B", Bold, Black], Style[ToString@B, Red]}
, {Style["C", Bold, Black], Style[ToString@C, Red]}
, {Style["centroid", Green], Style[ToString@N@centroid, Green]}
, {Style["circumcenter", Gray], Style[ToString@N@circumcenter, Gray]}
, {Style["incenter", Pink], Style[ToString@N@incenter, Pink]}
, {Style["orthocenter", Blue], Style[ToString@N@orthocenter[[1]], Blue]}
, {Style["ratio", Orange], Style[EuclideanDistance[orthocenter[[1]], centroid]/EuclideanDistance[circumcenter, centroid], Orange]}
}], Bottom]
]
]
, {{locA, p1}, Locator, Appearance -> None}
, {{locB, p2}, Locator, Appearance -> None}
, {{locC, p3}, Locator, Appearance -> None}
] // Quiet
Our function needs a list of three points. They will be the initial vertices of the triangle until you interactively move them with your mouse. It does not matter in which order you input the three points, the naming of the vertices will remain the same A, B, C in counter-clockwise direction. As you can see, the incenter does not lie on the Euler line.
pts1 = {{-1, 0}, {0, 5}, {2, 0}};
pts2 = {{-1, 0}, {2, 0}, {0, 5}};
pts3 = {{0, 0}, {-1, 2}, {2, 0}};
pts4 = {{3, -3}, {3, 3}, {-4, 2}};
triangleCentroids[pts4, PlotRange -> 5, Axes -> True]
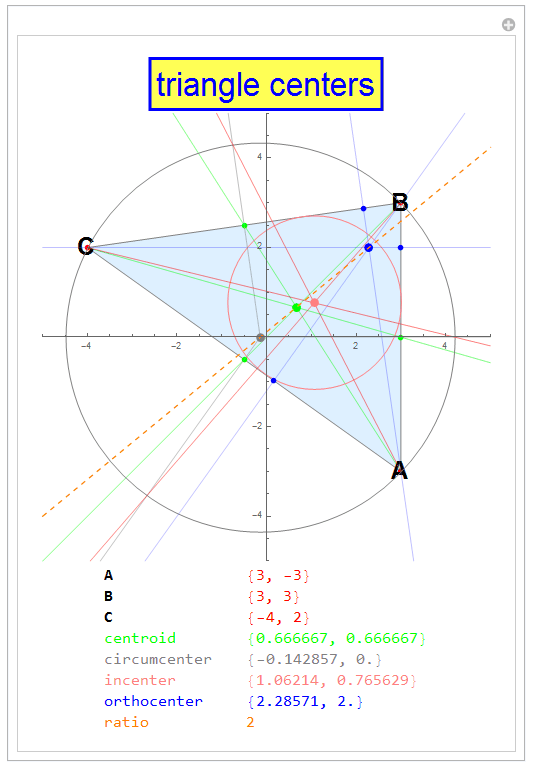
Remarkably, when you change the shape of the triangle, the relative distances between the centers is unchanged, with the ratio being 2:1, as demoed in the graphics. The structure of the code is very linear, straight-forward. It should be no problem for you to extend the code (graphics) by adding other centers or lines such as the nine-point-center, the de Longchamps point, and/or others.
As a personal comment, this exercise was very simple, since all of the code had been developed before, namely in exercise 11 of chapter 8.1. Here we only had to add code for the Euler line and for the legend. My above code is rather verbose with lots of variable definitions. But from watching many youtube tutorials on clean programming paradigms i learned that the urgently recommended professional-quality way of coding is not necessarily making the code either very efficient, very concise (least verbose), or admirably elegant, but making it as fast communicative as possible. Meaning, whoever reads your code (including your aged self in future! or your junior assistant) should be able to read and understand it right away (what is happening why in the code etc) in a fluent manner. In a real world situation or professional environment, time and full understanding is critical, is what matters (for code modifications, code extensions, modularization, sharing, debugging, recomposition, inheriting, team work, etc). The purpose of code is not primarily for making a machine do something but for communicating your concepts through the language of code, not only for the machine to understand! The clearer and easier you formulate them, in simpler terms, with simpler vocab items, the more readable and understandable it becomes for everyone who needs/must/wants to read and follow and work with you. No time is wasted by others (or yourself) on head scratchings over elegantly concise (but rather cryptic) code, and in the end the common end goal is achieved faster! This paradigm is also true in RL, for example when two non-native English speakers try/need to cooperate with each other in a critical situation but both persons have a different level of foreign language proficiency, e.g. level A2 vs C1. The C1-level speaker could express himself extremely accurately with a few perfectly matching words, however it would be worthless because communication would not take place, the A2-level speaker would not understand him. If the C1-level speaker didn't lower the communication level to the other person's level, both would fail together in the critical situation. I've been in this situation many times before, where i had to deal with lower language level colleagues: me trying to be more articulate, using higher level vocab items, didn't help them (they didn't understand me) nor it helped me (i couldn't get myself across). It was frustrating for me in several ways, but that's how the RL world works! If you want to communicate something important (through the language of speech or through the language of code), you must speak at the LCM (so to speak) of the target person, otherwise you(!) will fail too: you wanted to communicate your thought, but you failed to do so, because you chose the wrong communication level to start with. The boss comes in through the door, and only sees that you two didn't get the job done. The job is still unfinished. Dang!
Having said that, i hope you were able to understand my solution to the exercise, every bit of it. Making readers understand our ideas for a solution to an exercise is the very purpose of this public thread! There are more exercises in EPM for which the author did not post a solution. So let's keep this thread rolling :D