Message Boards Message Boards

0
|
8160 Views
|
3 Replies
|
2 Total Likes
View groups...
Share
Share this post:

Is there a way to add 'dimensions' on to multiple graphic objects?

Paul Cleary
Posted 12 years ago
I have tried adding text as such into the graphic part of the code in all possible places but can't get any lable to appear in the graphic.  I have included the code in its entirety rather than a snippet.  I would like to see the dimentions of the 4 triangles included on the graphic if possible.
 Clear[x,y,q,p];
 
 list=Reap[Do[p=Solve[x^2+y^2==q^2&&x>0&&y>0&&x<y,{x,y},Integers];
 
 p={x,y}/.p;
 
 k=Total@Flatten[p];
 
 If[k>0,Sow[Partition[Riffle[Flatten[p],q,{3,-1,3}],3]]],{q,5,1000}]];

list=Flatten[list[[2]],2];lst=SortBy[list,{#[[1]],#[[2]]}&];ml=Max[lst[[All,1]]];

flist=Reap[Do[g=Select[lst,#[[1]]==y&];

        Do[If[Length[g]>=2,j=Select[lst,#[[1]]==g[[q,2]]&]];

        k=Select[lst,#[[1]]==g[[w,2]]&];If[Length[j]<1||Length[k]<1,Continue[]];

        j1=Flatten[j];k1=Flatten[k];

        m=Take[j1,{2,-1,3}];

        m1=Take[k1,{2,-1,3}];

        m2=FromDigits[Intersection[m,m1]];

        r=Select[j,#[[2]]==m2&];

        t=Select[k,#[[2]]==m2&];If[Length[r]>0,Sow[{g[[q]],g[[w]],r,t}]],

        {q,1,Length[g]},{w,q+1,Length[g]}],

    {y,15,ml}]];

nflist={};flist=Partition[Flatten[flist[[2]]],12];simt=Reap[Do[If[flist[[q,2]]/flist[[q,1]]==flist[[q,11]]/flist[[q,10]],Sow[flist[[q]]],AppendTo[nflist,flist[[q]]]],{q,1,Length[flist]}]];

simt=Flatten[simt[[2]],1];

Do[AppendTo[simt[[q]],simt[[q,3]]+simt[[q,6]]+simt[[q,9]]+simt[[q,12]]],{q,1,Length[simt]}];Do[AppendTo[nflist[[q]],nflist[[q,3]]+nflist[[q,6]]+nflist[[q,9]]+nflist[[q,12]]],{q,1,Length[nflist]}];

nflist=SortBy[nflist,#[[13]]&];simt=SortBy[simt,#[[13]]&];

Print["Number of non similar triangles is ",Length[nflist]];

Print["Number of simmilar triangles is ",Length[simt]];

Do[Print[Partition[nflist[[q]],3,3,1,{}]];

t1={{0,0},{nflist[[q,1]],0},{0,nflist[[q,2]]}};

t2={{0,0},{nflist[[q,1]],0},{0,-nflist[[q,6]]}};

t3={{0,0},{-nflist[[q,8]],0},{0,-nflist[[q,6]]}};

t4={{0,0},{-nflist[[q,8]],0},{0,nflist[[q,2]]}};

Print[Graphics[{EdgeForm[Black],Red,Polygon[{t1}]

,EdgeForm[Black],Yellow,Polygon[{t2}],EdgeForm[Black],Cyan,Polygon[{t3}],EdgeForm[Black],Green,Polygon[{t4}]}]];Print[],{q,1,Length[nflist]}];Print[];Print[];

Print["Similar from here"];

Do[Print[Partition[simt[[q]],3,3,1,{}]];

t1={{0,0},{simt[[q,1]],0},{0,simt[[q,2]]}};

t2={{0,0},{simt[[q,1]],0},{0,-simt[[q,6]]}};

t3={{0,0},{-simt[[q,8]],0},{0,-simt[[q,6]]}};

t4={{0,0},{-simt[[q,8]],0},{0,simt[[q,2]]}};

Print[Graphics[{EdgeForm[Black],Red,Polygon[{t1}]

,EdgeForm[Black],Yellow,Polygon[{t2}],EdgeForm[Black],Red,Polygon[{t3}],EdgeForm[Black],Yellow,Polygon[{t4}]}]];Print[],{q,1,Length[simt]}];Print[];




The figures in the braces are the dimensions I would like inserting into the graphic.  

Paul.
POSTED BY: Paul Cleary
3 Replies
Sort By:
Hi Paul,

You can use Text["The text here",{x,y}] to insert text in your graphics. Your code looks really complicated, what is your input? What is that you are planning to do?
POSTED BY: Sander Huisman
Here is a simple effort to implement Sander's suggestion. As you can see length of the side is attached as a label to the side center and follows all transformations. 
Manipulate[Graphics3D[{{Opacity[.35], EdgeForm[Opacity[.35]],
    Cuboid[-d {1, 1, 1}, d {1, 1, 1}]}, {Red, PointSize[Large],
    Point[-{d, d, 0}]}, Text[Style[2 d, 17], -{d, d, 0}]},
    SphericalRegion -> True, RotationAction -> "Clip", PlotRange -> 2.3, Axes -> True
  ], {{d, 5/3}, 1/2, 2, 1/10, Appearance -> "Labeled"}]
POSTED BY: Vitaliy Kaurov
Paul Cleary
Paul Cleary
Posted 12 years ago
Thanks for your reply Sander, I played with your idea and got it to work to an extent, it just didn't have everything to display all I needed.  Regarding the input, it is self contained.  The program first calculates all Pythagorean Triangles with a hypotenuse less than 1000.  this bit  {q, 5, 1000}.  The remainder upto the graphic section looks for 4 PT's that share 2 sides each, such that the right angled corners can be plotted at a point.  It also sorts out similar and non similar triangles.

Thanks also to Vitaliy, I was able to pick out the required bits from your code and include them into mine with success.  What took a litte time to sort out were the order of plotting points so that previous points were not overdrawn by the next triangle, and also finding a scaling factor such that all looked equal regardless of the size of triangles.  I have included a cut down version that only plots the first non similar triangles.
 Clear[x, y, q, p]; list =
  Reap[Do[p =
     Solve[x^2 + y^2 == q^2 && x > 0 && y > 0 && x < y, {x, y},
      Integers]; p = {x, y} /. p; k = Total@Flatten[p];
    If[k > 0,
     Sow[Partition[Riffle[Flatten[p], q, {3, -1, 3}], 3]]], {q, 5,
     1000}]]; list = Flatten[list[[2]], 2]; lst =
  SortBy[list, {#[[1]], #[[2]]} &]; ml = Max[lst[[All, 1]]]; flist =
  Reap[Do[g = Select[lst, #[[1]] == y &];
   Do[If[Length[g] >= 2, j = Select[lst, #[[1]] == g[[q, 2]] &]];
    k = Select[lst, #[[1]] == g[[w, 2]] &];
    If[Length[j] < 1 || Length[k] < 1, Continue[]]; j1 = Flatten[j];
    k1 = Flatten[k]; m = Take[j1, {2, -1, 3}];
    m1 = Take[k1, {2, -1, 3}]; m2 = FromDigits[Intersection[m, m1]];
    r = Select[j, #[[2]] == m2 &]; t = Select[k, #[[2]] == m2 &];
    If[Length[r] > 0, Sow[{g[[q]], g[[w]], r, t}]], {q, 1,
     Length[g]}, {w, q + 1, Length[g]}], {y, 15,
    ml}]]; nflist = {}; flist =
Partition[Flatten[flist[[2]]], 12]; simt =
Reap[Do[If[
    flist[[q, 2]]/flist[[q, 1]] == flist[[q, 11]]/flist[[q, 10]],
    Sow[flist[[q]]], AppendTo[nflist, flist[[q]]]], {q, 1,
    Length[flist]}]]; simt = Flatten[simt[[2]], 1]; Do[
AppendTo[simt[[q]],
  simt[[q, 3]] + simt[[q, 6]] + simt[[q, 9]] + simt[[q, 12]]], {q, 1,
  Length[simt]}]; Do[
AppendTo[nflist[[q]],
  nflist[[q, 3]] + nflist[[q, 6]] + nflist[[q, 9]] +
   nflist[[q, 12]]], {q, 1, Length[nflist]}]; nflist =
SortBy[nflist, #[[13]] &]; simt =
SortBy[simt, #[[13]] &]; Print["Number of non similar triangles is ",
  Length[nflist]]; Do[
Print[Grid[Partition[nflist[[q]], 3, 3, 1, {}], Alignment -> Left,
   Frame -> All, Spacings -> {1, 1}]]; dp = nflist[[q, 8]]/25;
Print[Graphics[{EdgeForm[Black], Red,
    Polygon[{{0, 0}, {nflist[[q, 1]], 0}, {0,
       nflist[[q, 2]]}}], {Blue, PointSize[Medium],
     Point[{nflist[[q, 1]]/2, 0}]}, {Blue, PointSize[Large],
     Point[{0, nflist[[q, 2]]/2}]}, {Blue, PointSize[Medium],
     Point[{nflist[[q, 1]]/2, nflist[[q, 2]]/2}]},
    Text[Style[nflist[[q, 3]], Black, 17], {nflist[[q, 1]]/2 + dp,
      nflist[[q, 2]]/2}], EdgeForm[Black], Yellow,
    Polygon[{{0, 0}, {nflist[[q, 1]],
       0}, {0, -nflist[[q, 5]]}}], {Blue, PointSize[Medium],
     Point[{nflist[[q, 1]]/2, 0}]},
    Text[Style[nflist[[q, 1]], Black,
      17], {nflist[[q, 1]]/2, -dp}], {Blue, PointSize[Medium],
     Point[{0, -(nflist[[q, 5]]/2)}]}, {Blue, PointSize[Medium],
     Point[{nflist[[q, 1]]/2, -(nflist[[q, 5]]/2)}]},
    Text[Style[nflist[[q, 6]], Black,
      17], {nflist[[q, 1]]/2 + dp, -(nflist[[q, 5]]/2)}],
    EdgeForm[Black], Cyan,
    Polygon[{{0, 0}, {-nflist[[q, 8]],
       0}, {0, -nflist[[q, 5]]}}], {Blue, PointSize[Medium],
     Point[{0, -(nflist[[q, 5]]/2)}]},
    Text[Style[nflist[[q, 5]], Black,
      17], {-dp, -(nflist[[q, 5]]/2)}], {Blue, PointSize[Medium],
     Point[{-(nflist[[q, 8]]/2), 0}]},
    Text[Style[nflist[[q, 8]], Black,
      17], {-(nflist[[q, 8]]/2), -dp}], {Blue, PointSize[Medium],
     Point[{-(nflist[[q, 8]]/2), -(nflist[[q, 5]]/2)}]},
    Text[Style[nflist[[q, 12]], Black,
      17], {-(nflist[[q, 8]]/2), -(nflist[[q, 5]]/2) - dp}],
    EdgeForm[Black], Green,
    Polygon[{{0, 0}, {-nflist[[q, 8]], 0}, {0,
       nflist[[q, 2]]}}], {Blue, PointSize[Medium],
     Point[{0, nflist[[q, 2]]/2}]},
    Text[Style[nflist[[q, 2]], Black, 17], {-dp,
      nflist[[q, 2]]/2}], {Blue, PointSize[Medium],
     Point[{-(nflist[[q, 8]]/2), 0}]},
    Text[Style[nflist[[q, 8]], Black,
      17], {-(nflist[[q, 8]]/2), -dp}], {Blue, PointSize[Medium],
     Point[{-(nflist[[q, 8]]/2), nflist[[q, 2]]/2}]},
    Text[Style[nflist[[q, 9]], Black, 17], {-(nflist[[q, 8]]/2),
      nflist[[q, 2]]/2 + dp}]}, ImageSize -> {700, 700}]];
Print[], {q, 1, Length[nflist]}]



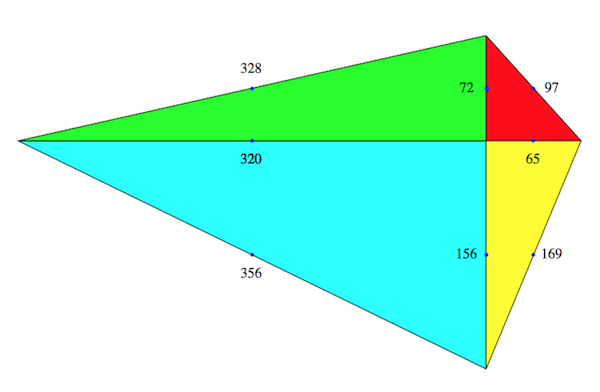
Thanks again for your quick replies and sorry i was late in replying.

Paul.
POSTED BY: Paul Cleary
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract