On 17 October 2018, Ivan Neretin discovered the octagonal dodecahedron, a toroid made from twelve octagons.

4, 6, 8 triangles can make a tetrahedron and up. The Snub Disphenoid has 12 faces.
6, 8, 9, 10 quadrilaterals can make a cube and up. The Rhombic Dodecahedron has 12 faces.
12, 16, 18, 20 pentagons can make a tetartoid or dodecahedron and up.
7, 8, 9, 10 hexagons can make make a Szilassi toroid and up.
12, 24 heptagons can make a heptagonal dodecahedron or Klein quartic 3-torus.
12 octagons can make an octagonal dodecahedron.

So how did I make that picture? First, I looked through the Canonical Polyhedra resource object for the outer polyhedron. The index turned out to be "8_9".

ResourceObject["Canonical Polyhedra"] 
ResourceData["Canonical Polyhedra"][["8_9"]] 

It's a geometric object with constraints since it's a canonical polyhedron. My WTC talk Narayama's Cow and Other Algebraic Numbers discussed how to use algebraic number fields to simplify geometrically constrained objects.

1. Get two or more points to simple fixed values.
2. Use RootApproximant[] on remaining points.
3. If remaining points have the same value for NumberFieldDiscriminant[coord^2], the object is in an algebraic number field.

Would the technique I suggested help to make the new object? Turns out it did.

I took the points from "8_9", kept the center at (0,0,0), found an EulerMatrix[] to forced the midpoints of two opposing edges to (0,0,1),(0,0,-1) and force those two edges to be parallel to the x,-y axes.

After using Chop[] in various ways to get 0, 1, and -1 values, I used RootApproximant[] on everything else, then looked at NumberFieldDiscriminant[coord^2] on all reasonable seeming values. The discriminant -104 turned out a lot, and soon I had all coordinates using the algebraic number field based on Root[#^3 - # - 2 &, 1].

I've found these functions useful for algebraic number fields.

FromSqrtSpace[root_, coord_] := Module[{ dim, degree, vector},
  dim = Dimensions[coord];
  degree = {1, 2}.NumberFieldSignature[root];
  vector = (root^Range[0, degree - 1]);
  Map[With[{k = (#).vector}, RootReduce[Sign[k] Sqrt[Abs[k]]]] &, coord, {Length[dim] - 1}]]; 

ToSqrtSpace[root_, coord_] := Module[{dim, order, algebraic},
   dim = Dimensions[coord];
   order = {1, 2}.NumberFieldSignature[root];
   algebraic = Map[Function[x, ToNumberField[Sign[x] RootReduce[x^2], root]], coord,{Length[dim] - 1} ];
   Map[Function[x, If[Head[x] === AlgebraicNumber, Last[x], PadRight[{x}, order]]], algebraic, {Length[dim]} ]];

The algebraic number field coordinates, actual coordinates, and faces.

valsV={{{0,1/2,-1/4},{0,0,0},{-1,0,0}},{{-2,0,1},{0,-2,1},{-1,2,-1}},{{0,2,-1},{2,0,-1},{1,-2,1}},{{0,2,-1},{-2,0,1},{1,-2,1}},{{-2,0,1},{0,2,-1},{-1,2,-1}},{{0,-1/2,1/4},{0,0,0},{-1,0,0}},{{0,0,0},{0,1/2,-1/4},{1,0,0}},{{0,0,0},{0,-1/2,1/4},{1,0,0}},{{2,0,-1},{0,2,-1},{-1,2,-1}},{{2,0,-1},{0,-2,1},{-1,2,-1}},{{0,-2,1},{-2,0,1},{1,-2,1}},{{0,-2,1},{2,0,-1},{1,-2,1}}}; 
p89v = FromSqrtSpace[Root[#^3 - # - 2 &, 1], valsV];
p89F={{1,2,3,4,5},{2,10,12,8,3},{4,7,11,9,5},{6,9,11,12,10},{1,5,9,6},{1,6,10,2},{3,8,7,4},{7,8,12,11}};

Code for the initial picture.

reg=RegionBoundary[RegionDifference[ConvexHullMesh[p89v],ConvexHullMesh[With[{a=.7, b=.6, c=.9},{{a,b,c}, {-a,-b,c},{-b,a,-c}, {b,-a,-c} }]]]];
DiscretizeRegion[reg,MeshCellStyle->{{2,All}->Opacity[.7]}, SphericalRegion-> True, ImageSize-> 600, ViewAngle-> Pi/10] 

Showing the original polyhedron and subtracted tetrahedron.

 Graphics3D[{EdgeForm[Thick], Opacity[.8], GraphicsComplex[p89v, Polygon[p89F]],
  With[{a = .7, b = .6, c = .9}, Polygon[Subsets[{{a, b, c}, {-a, -b, c}, {-b, a, -c}, {b, -a, -c} }, {3}]]]}, Boxed -> False, SphericalRegion -> True, ViewAngle -> Pi/9]

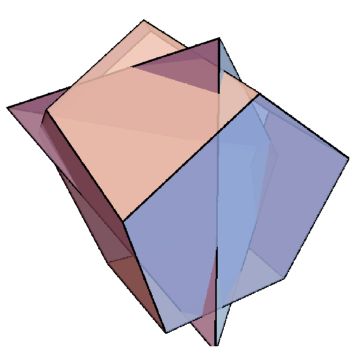
Might be possible to remove the canonical sub-polyhedron constraint and add a constraint that the octagons all have unit area. Or to minimize the ratio of largest/smallest edge.

If you'd like a hexagonal dodecahedron, here's a simple one.

DiscretizeRegion[RegionBoundary[RegionDifference[Region[Cuboid[{0, 0, 0}, {3, 3, 3}]], 
   RegionUnion[Region[Cuboid[{0, 0, 0}, {2, 2, 2}]], Region[Cuboid[{1, 1, 1}, {3, 3, 3}]]]]],
 MaxCellMeasure -> {"Area" -> 0.001}, AccuracyGoal -> 8, PrecisionGoal -> 8]

Attachments:

octagonalDodecahedron.nb