On 17 October 2018, Ivan Neretin discovered the octagonal dodecahedron, a toroid made from twelve octagons.
4, 6, 8 triangles can make a tetrahedron and up. The Snub Disphenoid has 12 faces.
6, 8, 9, 10 quadrilaterals can make a cube and up. The Rhombic Dodecahedron has 12 faces.
12, 16, 18, 20 pentagons can make a tetartoid or dodecahedron and up.
7, 8, 9, 10 hexagons can make make a Szilassi toroid and up.
12, 24 heptagons can make a heptagonal dodecahedron or Klein quartic 3-torus.
12 octagons can make an octagonal dodecahedron.

So how did I make that picture? First, I looked through the Canonical Polyhedra resource object for the outer polyhedron. The index turned out to be "8_9".
ResourceObject["Canonical Polyhedra"]
ResourceData["Canonical Polyhedra"][["8_9"]]
It's a geometric object with constraints since it's a canonical polyhedron. My WTC talk Narayama's Cow and Other Algebraic Numbers discussed how to use algebraic number fields to simplify geometrically constrained objects.
- Get two or more points to simple fixed values.
- Use RootApproximant[] on remaining points.
- If remaining points have the same value for NumberFieldDiscriminant[coord^2], the object is in an algebraic number field.
Would the technique I suggested help to make the new object? Turns out it did.
I took the points from "8_9", kept the center at (0,0,0), found an EulerMatrix[] to forced the midpoints of two opposing edges to (0,0,1),(0,0,-1) and force those two edges to be parallel to the x,-y axes.
After using Chop[] in various ways to get 0, 1, and -1 values, I used RootApproximant[] on everything else, then looked at NumberFieldDiscriminant[coord^2] on all reasonable seeming values. The discriminant -104 turned out a lot, and soon I had all coordinates using the algebraic number field based on Root[#^3 - # - 2 &, 1].
I've found these functions useful for algebraic number fields.
FromSqrtSpace[root_, coord_] := Module[{ dim, degree, vector},
dim = Dimensions[coord];
degree = {1, 2}.NumberFieldSignature[root];
vector = (root^Range[0, degree - 1]);
Map[With[{k = (#).vector}, RootReduce[Sign[k] Sqrt[Abs[k]]]] &, coord, {Length[dim] - 1}]];
ToSqrtSpace[root_, coord_] := Module[{dim, order, algebraic},
dim = Dimensions[coord];
order = {1, 2}.NumberFieldSignature[root];
algebraic = Map[Function[x, ToNumberField[Sign[x] RootReduce[x^2], root]], coord,{Length[dim] - 1} ];
Map[Function[x, If[Head[x] === AlgebraicNumber, Last[x], PadRight[{x}, order]]], algebraic, {Length[dim]} ]];
The algebraic number field coordinates, actual coordinates, and faces.
valsV={{{0,1/2,-1/4},{0,0,0},{-1,0,0}},{{-2,0,1},{0,-2,1},{-1,2,-1}},{{0,2,-1},{2,0,-1},{1,-2,1}},{{0,2,-1},{-2,0,1},{1,-2,1}},{{-2,0,1},{0,2,-1},{-1,2,-1}},{{0,-1/2,1/4},{0,0,0},{-1,0,0}},{{0,0,0},{0,1/2,-1/4},{1,0,0}},{{0,0,0},{0,-1/2,1/4},{1,0,0}},{{2,0,-1},{0,2,-1},{-1,2,-1}},{{2,0,-1},{0,-2,1},{-1,2,-1}},{{0,-2,1},{-2,0,1},{1,-2,1}},{{0,-2,1},{2,0,-1},{1,-2,1}}};
p89v = FromSqrtSpace[Root[#^3 - # - 2 &, 1], valsV];
p89F={{1,2,3,4,5},{2,10,12,8,3},{4,7,11,9,5},{6,9,11,12,10},{1,5,9,6},{1,6,10,2},{3,8,7,4},{7,8,12,11}};
Code for the initial picture.
reg=RegionBoundary[RegionDifference[ConvexHullMesh[p89v],ConvexHullMesh[With[{a=.7, b=.6, c=.9},{{a,b,c}, {-a,-b,c},{-b,a,-c}, {b,-a,-c} }]]]];
DiscretizeRegion[reg,MeshCellStyle->{{2,All}->Opacity[.7]}, SphericalRegion-> True, ImageSize-> 600, ViewAngle-> Pi/10]
Showing the original polyhedron and subtracted tetrahedron.
Graphics3D[{EdgeForm[Thick], Opacity[.8], GraphicsComplex[p89v, Polygon[p89F]],
With[{a = .7, b = .6, c = .9}, Polygon[Subsets[{{a, b, c}, {-a, -b, c}, {-b, a, -c}, {b, -a, -c} }, {3}]]]}, Boxed -> False, SphericalRegion -> True, ViewAngle -> Pi/9]
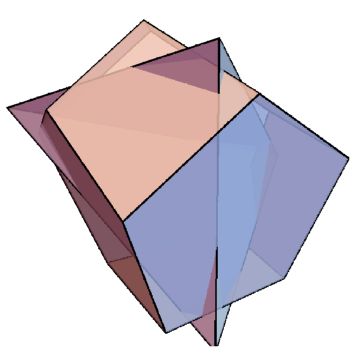
Might be possible to remove the canonical sub-polyhedron constraint and add a constraint that the octagons all have unit area. Or to minimize the ratio of largest/smallest edge.
If you'd like a hexagonal dodecahedron, here's a simple one.
DiscretizeRegion[RegionBoundary[RegionDifference[Region[Cuboid[{0, 0, 0}, {3, 3, 3}]],
RegionUnion[Region[Cuboid[{0, 0, 0}, {2, 2, 2}]], Region[Cuboid[{1, 1, 1}, {3, 3, 3}]]]]],
MaxCellMeasure -> {"Area" -> 0.001}, AccuracyGoal -> 8, PrecisionGoal -> 8]

 Attachments:
Attachments: