Group Abstract Group Abstract

Message Boards Message Boards

0
|
9.6K Views
|
10 Replies
|
8 Total Likes
View groups...
Share
Share this post:
GROUPS:
Mathematica

Mathematica Kernel crashes when evaluating Limit[ recursive function ]

Mario Weitzer
Posted 12 years ago
f[n_] := If[n == 1, 1, Sqrt[3 f[n - 1] - 1]]
Limit[f[n], n -> Infinity]

Evaluating these two lines makes the Mathematica 8.0 kernel crash.
POSTED BY: Mario Weitzer
10 Replies
Sort By:
One is stable, one is unstable, as you can see from the cob-web-plot above.

You mean 1/2 (3 + Sqrt[5]) is stable because both cob-web-plots reach it?
And 1/2 (3 - Sqrt[5]) is unstable because no cob-web-plot reaches it?

But you can easily reach the 1/2 (3 - Sqrt[5]) point by interchanging the role of the x = y line with the role of the function f: Starting at ?, stop first on the y = x line, turn left to the function, go down to the y = x line, turn left to the function and so on ... This modified procedure will not turn to an end if ? > 1/2 (3 + Sqrt[5]) because 1/2 (3 + Sqrt[5]) is the biggest crossing point between the y = x line and the function. So here is the orthodox cob-web-plot with the uF function:
POSTED BY: Udo Krause
Here are the cob-web-plots for this function:


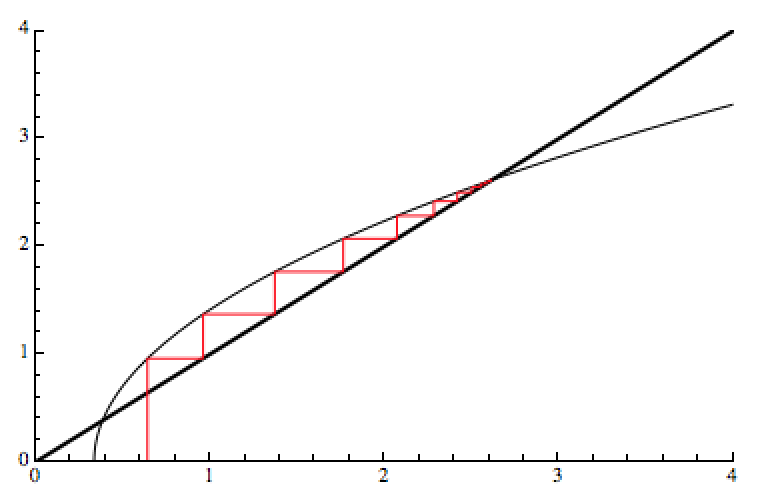
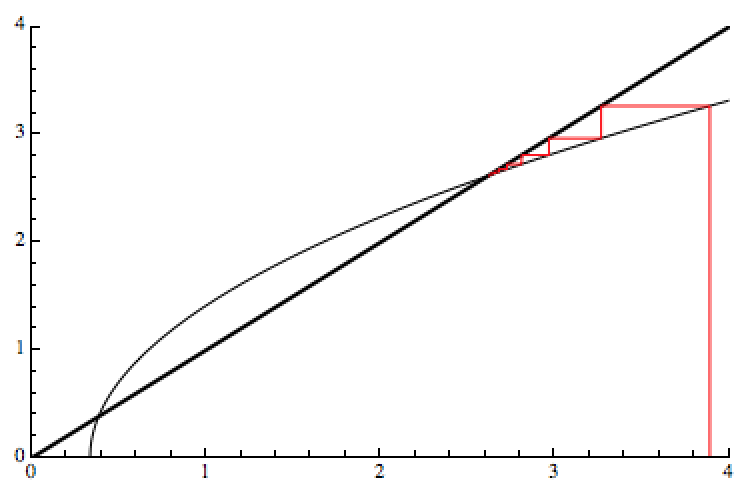
As you see there are two solutions:
1/2 (3 \[PlusMinus] Sqrt[5])

One is stable, one is unstable, as you can see from the cob-web-plot above.
Play around with it yourself using this code:
 ClearAll[CobwebPlot]
 SetAttributes[CobwebPlot,HoldAll]
 CobwebPlot[f_,start_?NumericQ,n_,{xrange:{xmin_,xmax_},yrange:{_,_}}]:=Module[{cob,x,g1,coor},
 cob=NestList[f,start,n];
 coor = Partition[Riffle[cob,cob],2,1];
 coor[[1,2]]=0;
 g1=Graphics[{Red,Line[coor]}];
 Show[{Plot[{x,f[x]},{x,xmin,xmax},PlotStyle->{{Thick,Black},Black },PlotRange->{xrange,yrange}],g1}]
 ]
Manipulate[CobwebPlot[Sqrt[3 #-1]&,\[Beta],50,{{0,4},{0,4}}],{{\[Beta],1},0,5}]
POSTED BY: Sander Huisman
You can get candidates for the limit simply by solving an equation for it.

In[83]:= candidates = limF /. Solve[limF == Sqrt[3*limF - 1], limF]
Out[83]= {1/2 (3 - Sqrt[5]), 1/2 (3 + Sqrt[5])}

One might ask what the 1/2 (3 - Sqrt[5]) candidate is for. In a way it belongs to the reverse directed weitzerF[], if on writes

weitzerF[n-1] (* arrrgh *) := Sqrt[3 weitzerF[n] - 1]

or with other words

 In[1]:= Remove[uF]
 uF[n_Integer?Positive] := uF[n] = (uF[n - 1]^2 + 1)/3
 uF[1] := 1
 
 In[4]:= uF[1]
 Out[4]= 1
 
 In[5]:= uF[2]
 Out[5]= 2/3

In[6]:= uF[3]
Out[6]= 13/27

In[7]:= uF[4]
Out[7]= 898/2187

In[9]:= uF[20] // N
Out[9]= 0.381966

In[14]:= RootApproximant[N[uF[25]], 2]
Out[14]= 1/2 (3 - Sqrt[5])

Mma 9.0.1. does not evaluate uF[30] in an useful span of time - because rational numbers with very big numerators and denominators are involved.
POSTED BY: Udo Krause
I think the main problem is, is that Limit will not go exactly over the integers. So it will never stop by the f[1] definition, because it might be f[1.56] or so that will be evaluated. 
The answer of Daniel is much more practical, and the correct way of solving this in my view.
POSTED BY: Sander Huisman
In[18]:= RootApproximant[FixedPoint[N[Sqrt[-1 + 3 #], 53] &, Sqrt[-1 + 3 Sqrt[2]]], 2]
Out[18]= 1/2 (3 + Sqrt[5])
POSTED BY: Udo Krause
You can get candidates for the limit simply by solving an equation for it.

In[83]:= candidates = limF /. Solve[limF == Sqrt[3*limF - 1], limF]

Out[83]= {1/2 (3 - Sqrt[5]), 1/2 (3 + Sqrt[5])}
The crash has been fixed for a future release. It will instead return unevaluated, as it should.
POSTED BY: Daniel Lichtblau
I used the Mathematica Kernel directly, so the error message showed.
In the Mathematica FrontEnd, the message does not come through. 
POSTED BY: Bruce Miller
If you do this right, it will not crash
 In[22]:= Remove[weitzerF]
 weitzerF[n_?Positive] := weitzerF[n] = Sqrt[3 weitzerF[n - 1] - 1]
 weitzerF[1] = 1;
 
 In[30]:= Limit[weitzerF[o], o -> \[Infinity]]
 Out[30]= Limit[weitzerF[o], o -> \[Infinity]]
 
 In[31]:= Limit[N[weitzerF[o]], o -> \[Infinity]]
 Out[31]= Limit[weitzerF[o], o -> \[Infinity]]

In[32]:= $Version
Out[32]= "9.0 for Microsoft Windows (64-bit) (January 25, 2013)"

but it does also not deliver a result. Therefore, if you do it even more right, you see that the very recursive nature of the weitzerF[] function tends to the usage of FixedPoint[]
 In[43]:= weitzerF[1]
 Out[43]= 1
 
 In[44]:= weitzerF[2]
 Out[44]= Sqrt[2]
 
 In[45]:= weitzerF[3]
 Out[45]= Sqrt[-1 + 3 Sqrt[2]]
 
In[46]:= weitzerF[4]
Out[46]= Sqrt[-1 + 3 Sqrt[-1 + 3 Sqrt[2]]]

and here is the limit
In[53]:= FixedPoint[N[Sqrt[-1 + 3 #], 53] &, Sqrt[-1 + 3 Sqrt[2]]]
Out[53]= 2.6180339887498948482045868343656381177203091798057628

Your original construction was misleading the kernel: The If[] contains a recursive function while n tends to infinity while nothing evaluates to a numerical value! Bad luck. Nonetheless the kernel should not crash and with newer versions it doesn't.
POSTED BY: Udo Krause
I don't get a segmentation fault on a Mac and Mathematica 9.0.1, but the limit does not evaluate either. 
I can, however, evaluate for example
f[n_] := Sqrt[3 f[n - 1] - 1]
f[1] = 1;
N[f[100], 20]
and then use
WolframAlpha[ToString[N[f[100], 20]],
IncludePods -> "PossibleClosedForm"]
That gives the result.
POSTED BY: Marco Thiel
duplicated here with 8.0.4 and 9.0.1 on Macintosh.

In[1]:= f[n_] := If[n == 1, 1, Sqrt[3 f[n - 1] - 1]]

In[2]:= Limit[f[n], n -> Infinity]
Segmentation fault

A dubious input, but the Kernel should not crash.
POSTED BY: Bruce Miller
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard