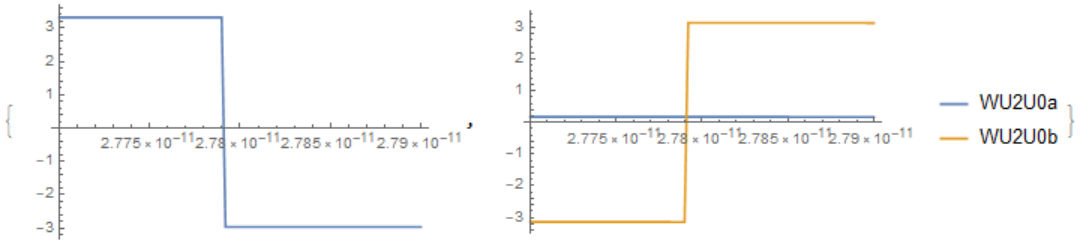Do not use C as a variable, since it is a built-in symbol in the system. We put X =WU2U0a - WU2U0b . In this problem we have a special case when X goes through 0 abruptly - see fig. Thus, all solvers fail on this problem. Fortunately, we can approximately determine the root of the equation as the minimum point X. It is possible that this solution makes sense for technical applications in trigger generators.

p = 9; Za = I*w*L + 1/(I*w*C1 + 2/Z0);
Zb = 1/(I*w*C1) + 1/(1/(I*w*L) + 2/Z0);
Zl = Re[1/(1/Za + 1/Zb)] - I*Im[1/(1/Za + 1/Zb)];
Zal = 1/(1/Zl + 1/Za);
Zbl = 1/(1/Zl + 1/Zb);
WU2U0a = Arg[Zbl/2/(1/(1/(Zbl + I*w*L) + I*w*C1) + Z0/2)];
WU2U0b = Arg[-Zal/
     2/(Z0/2 + 1/(1/(1/(Zal + 1/(I*w*C1))) + (1/(I*w*L))))];
Z0 = 44 - I*15; w = Rationalize[2*Pi*868*^6, 10^-p]; L = 18*^-10;
X = WU2U0a - WU2U0b;
Block[{$MinPrecision = p, $MaxPrecision = p}, 
 NMinimize[{X, 0 <= C1 < 5*10^-11}, C1, WorkingPrecision -> p]]
{-2.96652668, {C1 -> 2.77937850*10^-11}}
{Plot[X, {C1, 2.77`30*10^-11, 2.79`30*10^-11}], 
 Plot[{WU2U0a, WU2U0b}, {C1, 2.77`30*10^-11, 2.79`30*10^-11}, 
  PlotLegends -> "Expressions"]}

It is possible that some of the solutions found with MuPad are erroneous. It is easy to check, for example, that C1 = 1.606139208*10^-11 is not a root of the equation X = 0, indeed

In[3]:= X /. C1 -> 1.606139208*10^-11
Out[3]= 2.15442

Or have you found another solution? Does it coincide with mine C1 -> 2.77937850*10^-11?

It is a fact that there are many solutions for C1 that angle of transfer function 1 is equal to angle of transfer function 2. A German mathematician told me yesterday the problem is a quotient with 2 polynomials in w with the order 48.

It depends upon the methode to find some solutions. Different methods deliver different solutions. MuPad delivers 13 real solutions for C1. Mathematica's Solve and NSolve have different methodes, so it sometimes delivers different solutions depending on whether methode was internal used. -

Maybe I will check if there are wrong solutions when I have time.

I guess all solutions are right and we should accept that.

Regards Leo

In this problem, you compare impedances, not phases. This is another task, it has another solution in the complex plane. And in the original problem, we looked for real roots that physically correspond to the capacitance C1.

MuPad.pdf at the bottom in the graph shows that C1 is a correct solution to the problem. The two voltages are in phase in the load impedance, which we wanted. Please see also Zin and compare with Z0 at the top. There is adaptation with C1. I think Mathematica NSolve fails here because it does not provide all the real solutions. -

I also send You the basics to that problem with the circuit and the equitations.

Have fun - regards Leo

Attachments:

Balun0.pdf

MuPad.pdf