I've been trying to put together a double pendulum animation for my physics project.
forces = {m1*
x1''[t] == (\[Lambda]1[t]/l1) x1[t] - (\[Lambda]2[t]/
l2) (x2[t] - x1[t]),
m1* y1''[t] == (\[Lambda]1[t]/l1) y1[t] - (\[Lambda]2[t]/
l2) (y2[t] - y1[t]) - m1* g,
m2* x2''[t] == (\[Lambda]2[t]/l2) (x2[t] - x1[t]),
m2* y2''[t] == (\[Lambda]2[t]/l2) (y2[t] - y1[t]) - m2* g};
constraints = {x1[t]^2 + y1[t]^2 ==
l1^2, (x2[t] - x1[t])^2 + (y2[t] - y1[t])^2 == l2^2};
initialconditions = {x1[0] == 1, y1[0] == 0, x1'[0] == 0, y1'[0] == 0,
x2[0] == 1, y2[0] == -.6, x2'[0] == 0,
y2'[0] == 0}; constants = {g -> 9.8, m1 -> 1, m2 -> 1, l1 -> 1,
l2 -> .6};
solution =
First[NDSolve[{forces, constraints, initialconditions} /.
constants, {x1, y1, x2, y2, \[Lambda]1, \[Lambda]2}, {t, 0, 100},
Method -> {"IndexReduction" -> {"Pantelides",
"ConstraintMethod" -> "Projection"}}]];
Animate[
Graphics[{{PointSize[.025], {Gray, Point[{x1[t], y1[t]}]}, {Orange,
Point[{x2[t], y2[t]}]},
Line[{{0, 0}, {x1[t], y1[t]}, {x2[t], y2[t]}}]} /.
solution, {Orange,
Line[Map[Function[Evaluate[{x2[#], y2[#]} /. solution]],
Range[0, t, .025]]]}, {Gray, Opacity[.5],
Line[Map[Function[Evaluate[{x1[#], y1[#]} /. solution]],
Range[0, t, .025]]]}}, PlotRange -> {{-1.6, 1.6}, {-1.8, 0}},
Axes -> False, Ticks -> False, ImageSize -> 500], {{t, , "Time"}, 0,
7, .0000001}, DefaultDuration -> 40, RefreshRate -> 30]
I've been trying to export this using
Export["m.avi",%]
But the result I get is a 4 second long video that looks like this the entire time
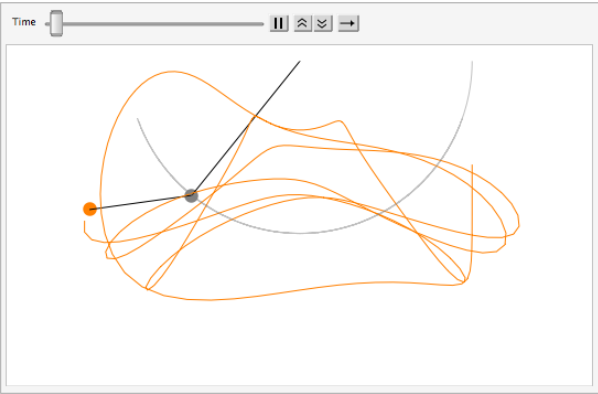
The output Mathematica gives after the animate command is the kind of thing i'm looking for -- a 40 second video of the double pendulum starting from the initial conditions of rest. Am I doing anything wrong?