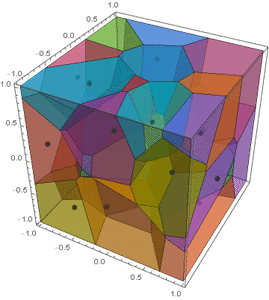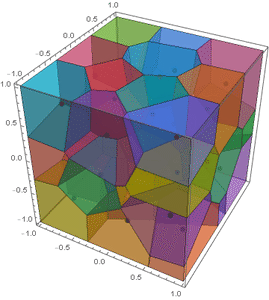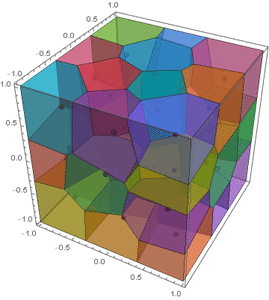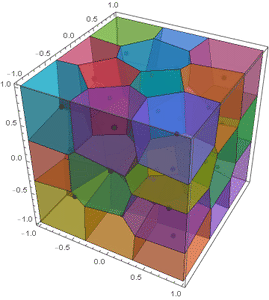
Chip and me were discussing his function a few days ago, when I mentioned to him that this can be used to implement Lloyd relaxation in 3D. In the spirit of this 2D Lloyd implementation and this spherical Lloyd implementation, I present the following:
VoronoiCells[pts_List, ibds : (_?MatrixQ | Automatic) : Automatic] /;
MatrixQ[pts, Internal`RealValuedNumericQ] &&
2 <= Last[Dimensions[pts]] <= 3 :=
Module[{bds, dm, conn, adj, lc, pc, cpts, hpts, hns, hp, vcells},
If[ibds === Automatic,
bds = CoordinateBounds[pts, Scaled[0.1]],
bds = ibds];
dm = DelaunayMesh[pts];
conn = dm["ConnectivityMatrix"[0, 1]];
adj = conn . Transpose[conn];
lc = conn["MatrixColumns"]; pc = adj["MatrixColumns"];
cpts = MeshCoordinates[dm];
vcells = Table[hpts = PropertyValue[{dm, {1, lc[[i]]}}, MeshCellCentroid];
hns = Transpose[Transpose[cpts[[DeleteCases[pc[[i]], i]]]] - cpts[[i]]];
hp = MapThread[HalfSpace, {hns, hpts}];
BoundaryDiscretizeGraphics[#, PlotRange -> bds] & /@ hp,
{i, MeshCellCount[dm, 0]}];
AssociationThread[cpts, RegionIntersection @@@ vcells]]
BlockRandom[SeedRandom["voronoi"];
pts = RandomReal[{-1, 1}, {32, 3}]];
lloyd = With[{maxit = 50,(*maximum iterations*)
tol = 0.005 (*distance tolerance*)},
FixedPointList[Function[pts,
RegionCentroid /@ Values[VoronoiCells[pts,
{{-1, 1}, {-1, 1}, {-1, 1}}]]],
pts, maxit,
SameTest -> (Max[MapThread[EuclideanDistance,
{#1, #2}]] < tol &)]];
frames = Function[pt, Show[MapIndexed[BoundaryMeshRegion[#,
MeshCellStyle -> {1 -> Black,
2 -> {Opacity[0.5],
ColorData[112] @@ #2}}] &,
Values[VoronoiCells[pt,
{{-1, 1}, {-1, 1}, {-1, 1}}]]],
Graphics3D[{PointSize[Large], Point[pt]}],
Axes -> True, Boxed -> True,
Method -> {"RelieveDPZFighting" -> True}]] /@ lloyd;
ListAnimate[frames]