No, you're not right, we made this replacement in (divsig0 /. uif -> uif[i - 1]) in line Do[
]. If you want to make this replacement earlier, then make it so that there is no error due to the coincidence of the names of the iterator
eaf[kk_] :=
Table[If[pcontour[[i, j]][[1]] +
uif[kk][t, pcontour[[i, j]][[1]], pcontour[[i, j]][[2]]] >
pillarscenters[[i, j]][[1]], t/100, 0], {i,
Dimensions[alpha][[1]]}, {j, Dimensions[alpha][[2]]}];
ear = Table[{eax[[i, j]] ea c1hs[ea, 10^(-6)],
eay[[i, j]] ea c1hs[ea, 10^(-6)]}, {i,
Dimensions[alpha][[1]]}, {j, Dimensions[alpha][[2]]}];
mesh = ToElementMesh[cell, MaxCellMeasure -> {"Length" -> 1 10^(-6)},
"BoundaryMeshGenerator" -> "Continuation"];
Ecell = 10^4;
EY1 = Ecell(**rigid+(Ecell/10)*soft*);
EY2 = Ecell/7;
nu12 = 0.3;
nu21 = 0.3;
G12 = EY1/(2*(1 + nu12));
ro = 1000;
lzonef = 2*10^(-6);
lzoner = -2*10^(-6);
zonef = c1hs[(x nppodx[[1, 1]] + y nppody[[1, 1]]) - lzonef, 10^(-12)];
zoner = c1hs[-(x nppodx[[1, 1]] + y nppody[[1, 1]]) + lzoner,
10^(-12)];
muv = 10^(16);
mustab = 10^(3);
mupil = 10^(9);
fadhf = muv*zonef*
c1hs[-dea, 10^(-10)] {D[u[t, x, y], t], D[v[t, x, y], t]};
fadhr = muv*zoner*
c1hs[dea, 10^(-10)] {D[u[t, x, y], t], D[v[t, x, y], t]};
fstab = mustab {D[u[t, x, y], t], D[v[t, x, y], t]};
fpillars = mupil {D[u[t, x, y], t], D[v[t, x, y], t]}*soft;
fadh = fadhf + fadhr + fstab;
mechprop = {Y -> EY1, \[Nu] -> nu12, rho -> ro};
\[Lambda]dp = Y \[Nu]/(1 + \[Nu])/(1 - 2 \[Nu]);
\[Lambda] = Y \[Nu]/(1 - \[Nu]^2);
\[Mu] = Y/2/(1 + \[Nu]);
\[CurlyEpsilon] = {{ix.Inactive[Grad][u[t, x, y], {x, y}],
1/2 (iy.Inactive[Grad][u[t, x, y], {x, y}] +
ix.Inactive[Grad][v[t, x, y], {x, y}])}, {1/
2 (iy.Inactive[Grad][u[t, x, y], {x, y}] +
ix.Inactive[Grad][v[t, x, y], {x, y}]),
iy.Inactive[Grad][v[t, x, y], {x, y}]}};
\[CurlyEpsilon]0[
kk_] := -ppods[[1,
1]] (eaf[kk][[1, 1]]) ((x nppodx[[1, 1]] + y nppody[[1, 1]])/
10^(-6))^2 {{nppodx[[1, 1]] nppodx[[1, 1]],
nppodx[[1, 1]] nppody[[1, 1]]}, {nppodx[[1, 1]] nppody[[1, 1]],
nppody[[1, 1]] nppody[[1, 1]]}};
\[Sigma] = \[Lambda] Tr[\[CurlyEpsilon]] Id +
2 \[Mu] (\[CurlyEpsilon]);
\[Sigma]0[kk_] := \[Lambda] Tr[\[CurlyEpsilon]0[kk]] Id +
2 \[Mu] (\[CurlyEpsilon]0[kk]);
divsig = {Inactive[Div][(\[Sigma].ix), {x, y}],
Inactive[Div][(\[Sigma].iy), {x, y}]} /. mechprop;
divsig0[kk_] := {Inactive[Div][(\[Sigma]0[kk].ix), {x, y}],
Inactive[Div][(\[Sigma]0[kk].iy), {x, y}]} /. mechprop;
inertia =
rho {D[u[t, x, y], {t, 2}], D[v[t, x, y], {t, 2}]} /. mechprop;
ci = {u[0, x, y] == 0., v[0, x, y] == 0.};
cid = {Derivative[1, 0, 0][u][0, x, y] == 0,
Derivative[1, 0, 0][v][0, x, y] == 0};
uif[0][t_, x_, y_] := 0
vif[0][t_, x_, y_] := 0
kf = 4; tf = 15;
Do[{uif[kk], vif[kk]} =
NDSolveValue[{Activate[divsig - divsig0[kk - 1] == inertia + fadh],
ci, cid}, {u, v}, {x, y} \[Element] mesh, {t, 0, tf},
Method -> {"PDEDiscretization" -> {"MethodOfLines",
"SpatialDiscretization" -> {"FiniteElement",
"MeshOptions" -> {"MeshOrder" -> 2,
"MaxCellMeasure" -> 0.5}, "IntegrationOrder" -> 4}}},
MaxStepSize -> 0.5];, {kk, 1, kf}]
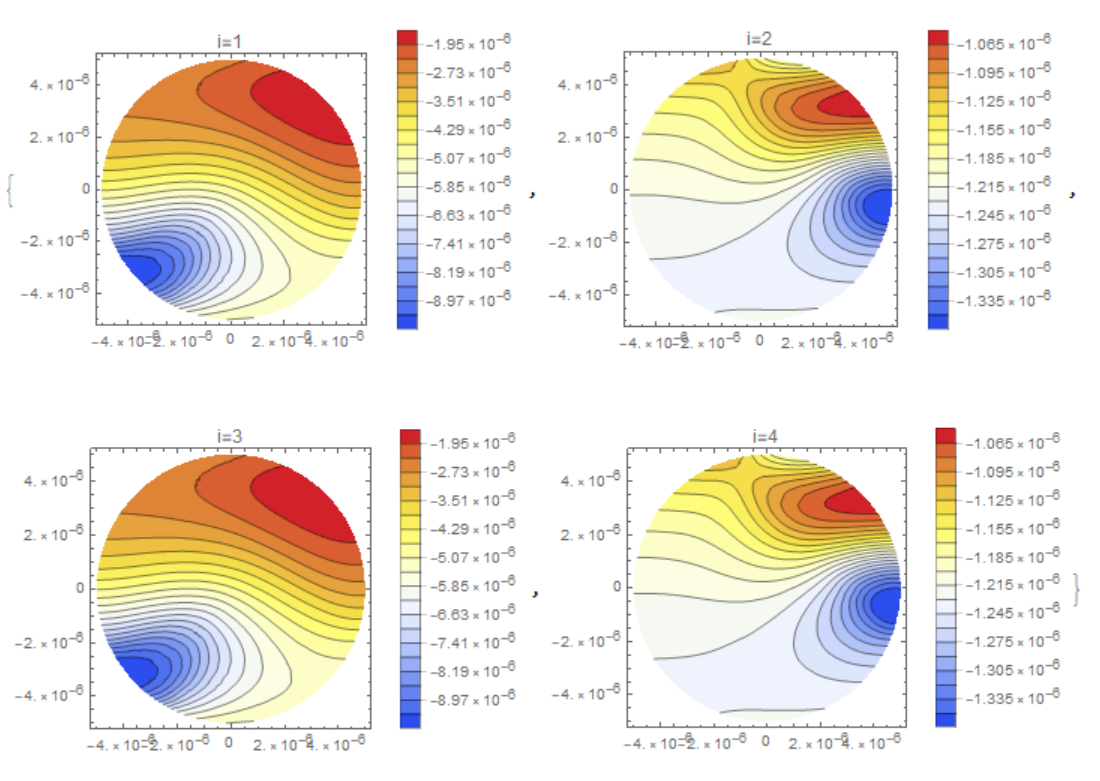
Table[ContourPlot[uif[i][tf, x, y], {x, y} \[Element] mesh,
PlotLegends -> Automatic, Contours -> 20,
ColorFunction -> "TemperatureMap", PlotLabel -> Row[{"i=", i}]], {i,
1, kf}]
 Attachments:
Attachments: