NOTE: click on the image to zoom-in; click browser back button to return to reading.

This is part of a series where I explore some of the videos of Numberphile, see also the other ones:
This one will be based on the Trinity Hall prime, see also the video here. 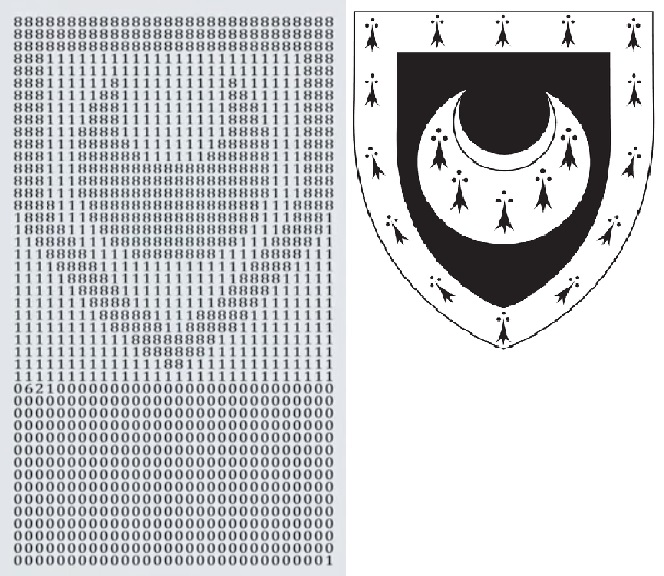
Where a logo was transformed to a large prime number.
Let's start with a christmas-themed snowflake:

Now we stretch and binarize this logo:
w = 100;
logo = ImageResize[logo, {All, Scaled[0.7]}];
pad = Ceiling[Min[ImageDimensions[logo]]/10];
logo = ColorNegate[ImagePad[logo, pad, White]];
logo = Binarize[ImageResize[logo, w]]
data = ImageData[logo];

For it to be a large prime without starting 0s, the first and large digit (pixel) should be a 1:
data[[1, 1]] = 1;
data[[-1, -1]] = 1;
Image[data]

Pay close attention to the top-left and bottom-right corner: they are now white.
If we now interpret this as a binary number, we can check if it is a prime:
PrimeQ@FromDigits[Join @@ data, 2]
False
Unfortunately not. Let's flip pixels around the edge (such that they are not easily noticed), perhaps finding a prime:
p1 = MorphologicalPerimeter[ColorNegate@logo];
p2 = MorphologicalPerimeter[logo];
p = ColorNegate@ImageMultiply[ColorNegate@p1, ColorNegate@p2];
p = DeleteBorderComponents[p];
flipindices = Flatten[Position[Join @@ ImageData[p], 1]];
number = Join @@ data;
Dynamic[ps]
Max[flipindices]
Do[
test = number;
test[[ps]] = 1 - test[[ps]];
test = FromDigits[test, 2];
If[PrimeQ[test], Print@test; Break[]]
,
{ps, flipindices} (* flip 1 pixel *)
]
Unfortunately, this also does not output anything. Changing 2 'bits':
number = Join @@ data;
Dynamic[ps]
Do[
test = number;
test[[ps]] = 1 - test[[ps]];
test = FromDigits[test, 2];
If[PrimeQ[test], Print@test; Break[]]
,
{ps, Tuples[flipindices, 2]} (* switch 2 pixels *)
]
This does output a large prime:
prime=10278724328516813380628067895662323773520449627379099305194765927606651462636820714912965905247759947431870939244784096072081224134673507412302862094348697137721205289662042749687699123575456824758923841258162456333389689959086563832197133456831196978237226561405122106854993716929980467602188871872201639193634149802209453340254150572297225285132770336160983436350465693751820298376232148117840341358912463502209407952972311633499178721039839656747451014343434021149297916568335540888361321284630136681997606668513504639856581590867592534754455119544795669540630073723155615797822396786083887035935497631159324587544753381711311848821996629979088458143585514437005799480572281670930263037708442541993407553293026958538828036156745551470364335036365968068482419462764393381134579328018832680301156300088187433903199783860765068309332582836994837504562317916193603397385380898275798608621501446214430050238630963428586750797746888119917853725017430333827393746136952282097698338379298307070659814996774606213456710941989583550377664823650637032881575420524241734010946827586537494888861898833009703587294907797917017236370736268403520480346607435631164517436908470324008042388379661782017968065905804376614125746685105699959529170568632602105119457634123388722108686001554026115921235994528708557027206141561632224298319037045461272948238877356833299514405600142589488863930553302309791459787698085697817810588979078033642563376678093835892370442883490584799133452599310751133704760810775856968881417084170157585220618114869525352603260028462891357045184371238340292965407931279812387104023889098730537404577287954468018818563224730195787462763934303079510477118479102356480917420242355474418049879289084930471229127175141123113756038037703772695569504177021429896856205611624796535916161954228581558273902091957780523425048024028971229158014831012639801257099484791882005628487071523763165462370822230153702005464201869547273471858320131558904543078406926712907685349742508757170373175165623118122539732954776173109480819681597052710849965958502408569893156757446968353405605821398623561844395369754266448549517974928186406045911934304257
Visualizing gives:
Image[Partition[IntegerDigits[prime, 2], w]]

Now making the visualization:
f=Sequence[FontFamily->"Menlo",FontSize->9];
chrs=Partition[IntegerDigits[prime],UpTo[w]];
h=Length[chrs]
chrs=MapIndexed[Text[Style[#1,f],{1,-1.4}Reverse[#2]]&,chrs,{2}];
binc=Partition[IntegerDigits[prime,2],UpTo[w]];
binc=MapIndexed[Text[Style[#1,f],{1,-1.4}Reverse[#2]+{0,-1.4 h-4.6}]&,binc,{2}];
gr=Graphics[{White,chrs,binc,Text[Style["is a prime number with "<>ToString[Length@IntegerDigits@prime]<>" digits",f],{5,-1.4h-2},{-1,0}],Text[Style["with the following base 2 representation",f],{5,-1.4h-4},{-1,0}]},Background->Black,ImageSize->850,PlotRangePadding->8]
Export["Logo_Prime_w"<>ToString[w]<>".pdf",gr]
Gives the image you can see at the top. Hope you enjoyed this little exploration! Now you can make your own prime-logos!